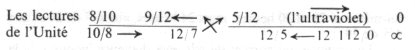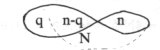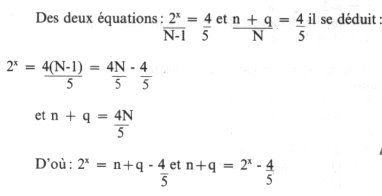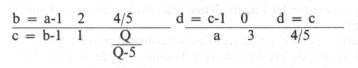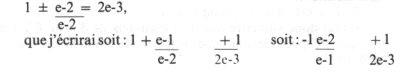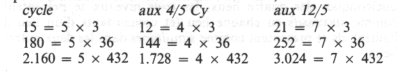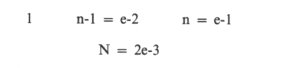8
LES SUCCESSIONS
J’ai montré, plutôt que démontré, que la Machine existe et que ses diverses lectures rendent compte de ses divers « états d’existence » dans l’étendue, la durée, l’espace et le temps. Epellantes, ces lectures sont d’accumulation dans le simultané (l’espace et le temps); révélatrices, elles sont de substitution dans le successif (l’étendue et la durée).
Je n’ai pas encore montré que la Machine fonctionne, c’est-à-dire que ses lectures déterminent non seulement ses diverses modalités (variations d’amplitude, dimensions de l’analemme) mais ses diverses relations avec les autres machines, contenues et contenantes.
Ou bien, la considérant comme une « monade » leibnizienne, j’ai décrit les principes (de causalité et d’acausalité entre autres) qui la déterminent en soi, ainsi que ses libertés, ses « degrés de liberté » propres, mais je n’ai pas prouvé que ces principes et ces libertés soient tels qu’ils déterminent et sont déterminés par une machinerie universelle, où toutes les machines concevables ne peuvent exister que l’une par l’autre.
Néanmoins, la définition de l’Unité – la seule acceptable – comme le produit de son quantum et de l’inverse de celui-ci : 1 = q X 1/q atteste qu’aucun objet n’existe comme contenant de ses parties ou composants sans exister comme contenu en un ensemble; et l’expérience nous révèle que, de même, aucun cycle n’est quantiquement définissable sans être l’inverse du quantum d’un cycle contenant. Le jour ne vaut pas 24 heures sans être le 1/30 du mois.
En extrapolant à la fois l’expérimentation cyclique et la formulation quantique de l’unité, il semble donc que définir un cycle en soi (à ses divers degrés de lecture) n’est qu’apparemment un autre problème que définir sa localisation dans l’ensemble des cycles. Mais les lois qui ordonnent l’extension (ou la réduction) de ses dimensions doivent correspondre de quelque manière à celles qui définissent sa position. Ni la coexistence des cycles ne doit être sans rapport avec leurs quantités de mouvements propres, ni leurs dimensions sans rapport avec la succession des cycles. Et, puisque leurs dimensions d’une part, leurs quantités de mouvements de l’autre apparaissent déterminées par leurs lectures, il faut que celles-ci, de même, déterminent la coexistence et la succession des cycles.
A cette condition seule nous pourrons affirmer que la machine fonctionne et que « cela marche ».
Cependant, la « théorie » purement mathématique sera notre seul guide en ces démonstrations. Outre le fait que peu de lecteurs y sont d’emblée disposés, on reconnaîtra que la « pure théorie » glace l’esprit, qu’elle l’absente de la réalité et que trop d’exemples la révèlent comme principal agent de l’erreur.
Une parenthèse, donc, semble nécessaire ici : l’étude circonstanciée d’une réalité que tous admettent : l’année des 12 mois dans le cycle des 12 ans. Hors de toute théorie, cela va sans le dire, et, sous les yeux, le calendrier chinois de l’année Xin-yu ou Année du Coq, 58ème année du 78ème cycle sexagésimal, fondé sur le mois lunaire (ou, plutôt, la lunaison), l’année des 12 mois et les cycles contenants que nous allons étudier.
L’année des 12 mois – Cette année – notre année 1981 – est la 58ème d’un cycle de 60 ans (5 X 12), dont l’achèvement, en 1983, complètera 78 cycles ou 4 680 ans depuis le 2ème avènement de l’Empereur Jaune (revécu dans la Connaissance/Justice), ce qui reconduit l’Avènement de notre « Bélier » en 2 697 avant J.-C.
Ce calcul, non étranger aux Tables de Confucius, révèle pour l’avènement de l’Empereur Blanc (2ème réveil), le temps de Confucius lui-même : -2697 + 2 160 ans = -537. Sans discuter l’exactitude du compte : -537 fut aussi l’époque de la fin de la captivité de Babylone (le Nouveau Temple), l’époque du Bouddha Gautama dans l’Inde, celle du premier Jésus en Juda, celle de Pythagore en Italie, d’Héraclite et de Parménide en Grèce, etc., je veux m’en tenir pour l’instant aux calculs non ésotériques qui précisent simplement l’Année dans sa durée d’une part, comme contenante du mois et contenue dans les 12 ans de l’autre.
Nous le savons : le calcul n’est pas simple.
Dans sa durée apparente, que je nommerai nominale, l’Année recouvre toujours les 12 mois. Ses degrés de lecture sont donc, sensiblement, les mêmes que ceux du mois. Soit au 1/12 près :
328/330 jours ou 12 mois lunaires,
360 jours ou 12 mois ésotériques,
364 jours ou tours de la terre sur elle-même,
365,25 jours grégoriens (pour 12 mois de 28, 29, 30 ou 31 jours).
Ces degrés de lecture, pourtant, sont suffisants pour rendre à peu près impossible la lecture des cycles contenants de l’Année : le cycle des 12 ans, puis celui des 60 (5 X 12), puis celui des 720 ans (60 X 12), puis celui des 4 320 ans ou deux ères précessionnelles (720 X 6), etc.
Le premier problème est évidemment de découvrir une grandeur commune aux différentes lectures de l’année.
Cette grandeur est de 6 940 jours.
En effet : 19 ans X 365,25 = 6 939,75 jours, et 19 X 365 jours 6 heures 9’9″ » = 6 940.
235 mois X 29,53 (la lunaison) = 6 940 jours,
252 mois X 27, 53 (le mois linaire) = 6 940 jours.
Comme 19 ans également 228 mois grégoriens, c’est-à-dire que :
228 mois grégoriens = 235 lunaisons = 252 mois lunaires.
Les 228 mois grégoriens égalent 19 ans solaires,
les 235 lunaisons égalent 19 ans et 7 mois lunaires,
les 252 mois lunaires égalent 21 ans de 330 jours.
Si je veux ramener le calcul au 1/12, puisque le « mois » est le 1/12 de l’année et l’année le 1/12 du cycle supérieur, je trouve : 6940/12 = 578,33 jours et ce nombre : 578,33 me semble dénué de toute signification. Il représente pourtant 21 mois lunaires de 27,57 jours.
Puis, si je partage l’année lunaire (12 X 27,57 = 330,84 jours) en 4 saisons, je trouve que la « saison » lunaire égale 82,7 jours.
578,9 jours égalent 7 de ces saisons ou une année lunaire trois-quarts.
Je dois me rappeler alors que le calendrier chinois actuel n’est qu’une déformation d’un calendrier plus ancien, qui jouait de 5 et non de 4 saisons :
82,71 X 4 = 330,84 jours, l’année lunaire ou 4 « saisons »,
82,71 X 5 = 413,55 jours, l’année mythique ou 5 « saisons »,
82,71 X 7 = 578,97 jours ou 7 « saisons » (21 mois lunaires).
L’année lunaire n’est donc qu’une lecture aux 4/5 ou 8/10 d’un cycle de 5 saisons.
Si je considère 413 jours comme la durée réelle du cycle, aux 12/7 ou (e-1) du cycle, l’alternative 7/5 me donne :
241 ans d’unité + 172 ans de dégénérescence = 413.
Les 5/12 de 578,97 égalent précisément 241 jours. Si bien que 578,97 est également la lecture aux 12/5 de l’unité : 241.
Ces nombres rendent compte à la fois des « apparences » du cycle, à ses divers degrés de lecture, et de sa « durée » aux 12/7. Mais rendent-ils compte de sa position contenue/contenante?
Les nombres répondent :
82,71 jours (la « saison » de l’année lunaire) donnent :
au 1/12 : 6,9 jours, c’est-à-dire la semaine dans le mois, multipliés par 12 : 3 ans, c’est-à-dire le quart de l’activité solaire, sur 12 ans.
Les 12 ans reconduisent aux 60 du cycle sexagésimal (5 X 12); les 60 aux 360 ans (6 X 60) et aux 720 ans (12 X 60), les 360 et les 720 aux 2 160 (6 X 360 ou 3 X 720), etc.
Nous obtenons un décompte qui tient compte de la semaine et de l’année lunaire, des lunaisons, du cycle des 12 ans, des « saisons » de l’ère précessionnelle et de cette ère, des « saisons » de la Grande Année et de la Grande Année, en poursuivant, etc.
Mais ce n’est plus seulement par le jeu des « lectures », c’est par l’intégration des 4/5 ou 8/10, des 12/7 (la durée du cycle), des 12/5, etc. Le tout contenu dans la Machine :
Autres calculs – Rien n’interdit que je renouvelle la même démonstration (ou, sinon la même, une très analogue) sur des exemples différents : le calendrier sumérien ou le calendrier hindouiste, le maya-quiché ou le grégorien. Il s’agira toujours d’un jeu entre diverses lectures d’un cycle (lunaire ou solaire, généralement) desquelles seront déduits des cycles plus étendus.
Généralement aussi, d’une construction à l’autre, les nombres mêmes apparaitraient peu différents. Un ésotérisme traditionnel donne : 210 pour 241 (l’Unité) et 150 pour 172 (sa corruption), donc 360 pour 413 (210 + 150) et 504 aux 12/5, pour 578,33. Puis, au cycle douze fois supérieur : 2 520 (pour 2 892), 1 800 (pour 2 065) et leur somme : 4 320 pour 4 957; 6 048 pour 6 940, aux 12/5;
Ces nombres autorisent à considérer l’année comme un cercle de 360 degrés d’un jour chacun, et le cycle a.s. comme un cercle de 360 degrés de 12 jours chacun.
Plus surprenant est le fait que les diverses sciences contemporaines n’ont pas inventé une autre méthode d’approche de la réalité que ce recours aux 360 degrés et ce transfert d’une constante à l’autre (comme l’h barré n’est que le rayon de la circonférence h). C’est qu’il s’agit de l’opération la plus banale, que j’effectue plusieurs fois par jour, quand je parle d’un bâton comme d’une unité, bien qu’il soit un fragment de la branche, ou de l’heure comme une telle unité, bien qu’elle ne soit que le 1/12 de l’horloge, etc.
Le jour lui-même, est-il le 1/7 de la semaine et le 1/28 du mois lunaire ou le 1/30 du mois ésotérique? J’en parle comme s’il était l’un et l’autre.
En tant que 1/30 du mois, il est aussi le 1/360 de l’année; mais il ne l’est plus en tant que 1/28 du mois lunaire. Puis, il ne contient lui-même ni 28 ni 30 heures, mais 24 heures, aux 6/7 de 28 et aux 4/5 de 30.
Le principe qui permet de tels jeux demeure inconnu de la majorité des hommes (malheureusement, puisque y réside la seule déterminante relativité). Mais il n’est pas autre, en réalité, que le principe de l’interaction de toute lecture et de tout délit (ou de toute information et de toute entropie), puisque l’existence est un tel délit et que je dois, en effet, exister avant de lire : cogito, ergo sum.
Or, nous savons qu’exister, c’est nécessairement se localiser en cette phase de sa propre durée que détermine une constante quelconque et où l’unité ne s’offre à « moi » que comme une lecture de ladite phase.
De cette unité fictive, ou du moins relative, et de la constante qui la détermine (h barré ou tau-1, tau ou e-1) se déduiront donc tous les calculs par lesquels je prétendrai embrasser l’univers : de tau les puissances de tau (ou de 10 les puissances de 10, équivalentes), de θ+1, 12(θ+1) et, de π, 10π, qui s’équivalent.
Ici, tous les jeux s’imaginent, comme la période du carbone 14, sur la base 1/(e-1), ou les durées de l’humanité, de la vie, de la matière, sur les puissances de 10. Mieux : ils se réalisent, comme les 49 ans sabbatiques ou les 19 ans coraniques, les 52 ans des Aztèques, nos 40 heures hebdomadaires, nos 8 heures de travail quotidien. Le cycle imaginaire remplace le cycle réel, comme la « semaine » le quartier lunaire ou la « moyenne » des 11,1 ans le cycle d’activité solaire en son extrême complexité.
Ce serait une grave erreur que ne voir dans ces inventions ludiques qu’un phénomène ésotérique ou religieux. Plusieurs exemples récents nous prouvent qu’il s’agit là d’un besoin permanent de l’esprit, dès que l’esprit entend s’exercer.
Exemple : les Anciens croyaient que tous les corps obéissent à certains rythmes cycliques d’attraction et de répulsion. Notre 18ème siècle a raillé ces croyances, en démontrant que certains corps produisent une électricité positive et d’autres une électricité négative (vitreuse/résineuse). Puis, le 19ème siècle a raillé ces nouvelles croyances, car tous les corps sont constitués des mêmes particules, atomiques hier, subatomiques aujourd’hui, et ces particules apparaissent comme liées à des cycles déterminés, selon leur charge, positive ou négative, sinon à des orbites, selon qu’elles s’éloignent ou se rapprochent du noyau. Si bien qu’aujourd’hui, ce ne sont plus les corps seulement que nous considérons comme axés, mais leurs composants invisibles.
Autre exemple : en de certaines périodes de l’Histoire, les maladies « épidémiques » ont pu être considérées comme liées à des cycles contenants (planétaires); en d’autres périodes, telles que la fin du siècle dernier, comme liées à des cycles d’activité ou d’inertie microscopiques; et, de nouveau, en notre époque, à des cycles contenants et mal connus (sociologiques ou biologiques).
Troisième exemple : l’ancien Grec croyait que le soleil tourne autour de la terre en vingt-quatre heures. Il n’avait donc aucun besoin de l’année, dont la succession saisonnière lui prouvait pourtant l’existence. Nous croyons aujourd’hui que ce cycle annuel démontre la rotation de la terre autour de notre soleil, cependant que le cycle circadien ne prouve que la rotation de la terre sur elle-même. Si la terre n’est pas immobile, de nombreuses croyances en découlent, qui constituent notre univers mental (dont la constance de la vitesse de la lumière, après les expériences de Michelson et de Morley). Mais ni la rotation de la terre sur elle-même ni sa révolution autour de notre soleil n’expliquent les mouvements apparents de l’astre. D’autres hypothèses ont donc vu le jour, depuis le 3ème mouvement terrestre de Kepler jusqu’au mouvement du système solaire à travers notre galaxie. De sorte qu’aujourd’hui, ce n’est plus le soleil seulement mais le cosmos tout entier qui tourne autour de la terre, elle-même non plus immobile il est vrai.
L’ironie, en somme, ne naît pas de la constatation du cycle, que personne ne met en doute, mais de ses interprétations successives, selon qu’on le considère comme contenant ou contenu. Plus profondément, il se peut que la raillerie s’alimente de la passion qui anime les chercheurs : que quelque chose, le soleil, la planète, la lumière ou la particule revienne identiquement au terme d’un cycle défini. Car, alors même qu’il nie le Retour, le plus sceptique des esprits ne se libère pas longtemps de son besoin : s’il n’attend plus le retour du paradis perdu, il croit en celui du premier Bang.
Le retour éternel
Le retour éternel peut être défini comme le retour du Même au terme d’un même temps ou dans un même espace.
I – Dans l’espace :
a) le Même peut être la chose même. Par exemple, cette unité-là d’un homme : JE, ou la lune en soi, le soleil en soi.
En ce sens, il est certain que le Même revient ou peut revenir un grand nombre de fois au même lieu, mais il y revient en des états différents de sa durée : JE en son enfance, sa maturité, sa vieillesse, dans ce même village ou cette même chambre; ou telle planète en soi en un même point de l’espace, mais la lune par exemple en son premier quartier, sa plénitude, son dernier quartier, son renouvellement. Ou le soleil chaque année de son cycle d’activité, mais dans la croissance ou la décroissance de cette activité même.
Tous les cycles, en ce sens, se ramènent à une alternance définie : de croissance formelle (par le réchauffement) et de décroissance formelle (par le refroidissement), ou de cohérence massique (par le refroidissement) et d’incohérence massique (par le réchauffement), etc.
La chose même revient au même lieu, mais ce n’est pas la même chose.
b) Dans l’espace également, le Même peut être la même chose, dans la mesure où deux Personnes ou deux planètes semblent passer par les mêmes états. En ce sens également, deux mêmes choses peuvent se retrouver au même lieu, dans le même état : toutes les planètes du système solaire à l’est ou à l’ouest du soleil, et ce peut être dans la même phase de croissance ou de décroissance.
Mon père, puis moi, puis mon fils, nous pouvons nous être retrouvés dans la même chambre, en notre enfance tous les trois.
Mais les planètes différentes ne se retrouvent pas sur la même orbite; ni mon père et moi au même endroit dans la chambre et dans la même lumière. Ou bien, si cette coïncidence survient, elle ne peut être que hasardeuse et sans la moindre conséquence causale.
La théorie sera toujours que deux mêmes choses, dans le même état, ne se retrouvent jamais exactement au même lieu (ne serait-ce que parce que, d’un passage à l’autre, le lieu s’est modifié).
Il reste que, dans le premier cas, je pourrai parler de retour (à une approximation près, liée à la différence d’états de la chose même), en me fondant sur le 1/2, dans l’alternance; et que, dans le second cas, je pourrai parler aussi de retour (à une approximation près, liée à la relativité de l’analogie entre les deux mêmes choses), en me fondant sur le double ou le 2.
II – Dans le temps :
a) Un même intervalle de temps peut signifier « entre deux états identiques », par exemple, entre deux premiers quartiers de lunaisons successives, ou entre deux printemps ou entre deux enfances. Je dirai que les deux premiers quartiers se suivent avec un intervalle de 29,5 jours, les deux printemps avec un intervalle de 365,25 jours, les deux enfances avec un intervalle d’une génération.
Mais deux cycles successifs ne présentent pas la même succession d’états : ce premier quartier dure 7 jours et le suivant 8 jours; ce printemps est plus bref ou plus long que le précédent (de plusieurs jours); ce fils est né vingt ans après son père, celui-là trente-cinq ans plus tard.
Si bien que deux intervalles de temps entre trois mêmes états successifs ne seront jamais exactement les mêmes.
b) Un même intervalle de temps peut également signifier « entre deux étants, successifs ou non », par exemple entre deux mois lunaires d’exactement 27,33 jours ou deux vies de 65 ans. Tous les calendriers se fondent sur cette illusion que tous les jours comportent 24 heures ou toutes les années 12 mois.
Mais un jour n’est qu’un état du cycle lunaire ou saisonnier : il compte plus ou moins 24 heures au cours de la saison, comme le prouve l’expérience du Massachusetts; une année n’est que l’état d’un cycle plus grand, que les Anciens Romains dénombraient par 1 461 jours (3 ans de 365 jours et 1 an de 366 jours) et les Egyptiens par 1 461 ans.
En fait, tout le calcul se fonde ici sur le morcellement quantique du cycle, en 12 ou 24, 30 ou 60 parties, le degré de liberté étant d’autant plus faible que le quantum choisi est plus grand.
On le vérifie par les trois calculs du mois : le mois solaire, le mois lunaire et la lunaison. Les trois s’identifient en 6 940 jours : 228 mois solaires, 235 lunaisons, 252 mois lunaires, selon que le quantum choisi est 6 940 sur 228, 235 ou 252, le degré de liberté le moindre étant celui du mois lunaire.
Mais, pour autant, parlera-t-on de retour éternel au terme des 1 461 ans égyptiens ou des 6 940 jours?
On doit se référer ici à la loi de Pierre Curie : « dans l’addition de plusieurs systèmes de phénomènes, les symétries ne s’ajoutent pas, seulement les dissymétries ». Il en va de même pour les cycles contenus l’un dans l’autre.
Si deux cycles successifs ne sont jamais exactement les mêmes (puisqu’ils ne sont que des états d’un cycle plus grand, en la durée de celui-ci), comment deux cycles non successifs pourraient-ils être exactement les mêmes (états alors d’étants qui ne sont que des états d’un cycle infiniment plus grand)?
Non seulement le cycle formule un mouvement : par exemple d’une planète autour du soleil, mais il formule le mouvement interne du cycle, comme de la pleine lune au dernier quartier dans le mouvement lunaire ou comme du maximum de réchauffement au maximum de refroidissement dans le mouvement terrestre (ou dans le mouvement propre au sommeil humain).
La lecture de l’un (contenu ou contenant) l’emporte toujours sur l’autre, soit de la lunaison soit du mois lunaire, soit de l’activité solaire soit de la conjonction Jupiter-soleil par exemple. Le choix du contenant (quantique) comme du jour de 24 heures ne correspond jamais qu’à un degré de liberté près avec le choix du contenu (le jour dans l’analemme saisonnier).
Le mouvement – Je peux donc avoir du mouvement deux visions opposées : soit d’un mouvement qui emporte la chose, comme un tapis où se succéderaient les couleurs et les formes ou comme un film qui se déroule et se projette en se déroulant, soit de quelque évolution/involution, diastole/systole, jour/nuit.
Soit des choses différentes qui se présentent successivement, linéairement, le long du tapis volant ou du trottoir roulant; soit les mêmes choses qui se présentent différemment pendant l’aller et le retour de la balançoire.
Si je parle de temps contenant et contenu, le contenant peut se présenter comme un mouvement-trottoir (aussi longtemps que j’ignore son propre contenant), comme j’imagine la course de notre galaxie à travers le cosmos ou la durée radioactive de l’électron dans l’inconcevable réalité; mais le temps contenu, dont je connais le contenant, se présente toujours à moi comme un temps-balançoire, en ce moment précis de son balancement.
Si je parle de retour, il me faut reconnaître que, dans le premier cas, il exige que le temps-trottoir soit circulaire, afin que je repasse par où je suis passé; que, dans le second cas, il exige que le balancement soit régulier, replaçant à nouveau les choses sous le même angle et dans la même lumière.
Mais, dans les deux cas, on voit que je demeure soumis à des lois : ou la loi de ma durée-trottoir, qui m’emporte, du devenir au devenu toujours, ou la loi du temps-balançoire qui, dans le jour, l’année, le cycle d’activité solaire, etc., me promène du haut vers le bas, du refroidissement au réchauffement, ou de l’excès de calcium au manque de calcium, et inversement, selon la fréquence et l’amplitude du balancement.
Egalement, le monde m’apparait différent, soit qu’il ne cesse de s’obscurcir ou de s’affadir au long de ma durée-trottoir, soit que périodiquement il retrouve couleur et vie en chaque aurore, à chaque printemps, à chaque maximum solaire.
L’illusion, bien sûr, est de s’attacher aux renversements de la balançoire alors que, seul, le trottoir-durée m’emporte. Ou, du moins, c’est là l’illusion de la vie, sans laquelle je n’accepterai pas de vivre. Mais n’y aurait-il pas une illusion de la mort, fin de toute durée, alors que, de toute évidence, toute durée n’est qu’un moment du balancement qui la contient, comme l’alternance jour/nuit contient 9 331 200 vibrations au 1/100 de seconde, la seconde 9 331 200 vibrations du césium ou l’année 9 331 200 pleines respirations?
Il se trouve seulement que chaque être habite sa durée : le césium le 1/9 331 200 de la seconde, le microbe que mon souffle expulse le 1/9 331 200 de l’année, et mon expiration-durée, que je nomme ma vie, le 1/9 331 200, peut-être, d’un autre cycle, que je ne peux même concevoir.
Pas plus que les formes (leurs apparences) dans l’étendue ne me révèlent le véritable espace, contenu dans le plus petit contenu concevable, la matière du temps (la durée) ne me révèle le temps véritable, contenant du plus grand contenant imaginable, à l’infini.
La cohérence et le discernement – L’usage n’est pas de considérer l’Espace comme le plus petit contenu et le Temps comme le plus grand contenant. La conception contemporaine unit la notion de forme et celle d’espace; la notion de matière (masse/énergie) et celle de temps.
Mais on peut seulement dire :
a) que les apparences formelles ont toutes une étendue, en tant qu’elles sont discernables,
b) que les énergies matérielles ont toutes une durée, en tant qu’elles sont cohérentes.
Nous savons maintenant qu’il est des formes totalement incohérentes (dans le hasard, ou le jeu ou l’acausalité, la pœdomorphose ou le fractal, ou la particule non polarisée), contingentes alors mais aussi contingentées, c’est-à-dire localisées, comme le boson, au double (spin : 2) sur la dernière orbite;
et qu’il est des matières (masse/énergie) totalement indiscernables, comme les ions-électrons eux-mêmes (de spin 1/2) sinon leur accumulation (le trou noir).
Mon hypothèse est double : que l’Espace n’est peut-être que cette matière indiscernable (hypothèse admise aujourd’hui) et que le Temps n’est peut-être que cette forme incohérente mais contingentée, dans la contingence; inerte et, par suite, de masse nulle.
Il s’ensuit que, considérés du point de vue d’un cycle étendue/durée, ma vie, quelque chose précède le cycle et que cette chose est le Temps, quelque chose suit le cycle ou lui survit et que cette chose est l’Espace.
Les Anciens situaient ce Temps formel depuis l’infini jusqu’à 2. Il convient peut-être de le situer depuis l’infini jusqu’à tau = 2,154, tel que tau ³ = 10, tau ⁶ = 100, tau⁹ = 1 000, etc.
Les Anciens situaient cet Espace matériel depuis 1/2 jusqu’à 0 (depuis Hésiode jusqu’à la Table Gardée de l’Islam). Il convient peut-être de le situer hors de la couleur visible, de 0,4 (ou 5/12) à 0.
La formule – De toute façon, jusqu’à présent, aucune formule mathématique n’apparaissait commune aux quatre lieux : le Temps et l’étendue, la durée et l’Espace. Mais toutes les constantes mathématiques découvertes depuis 4 000 ans se rattachent aux constantes : tau-1 = 1,154, √e-1 = 1,309, θ = 1,618, √5, etc.
Par exemple, π = (12 (θ+1))/10
e-1 = (√e-1)²
N (le nombre d’Avogadro) = 2(tau+1)
h (la constante de Planck) = (4π)³/C
etc.
Et toutes ces constantes « primordiales » sont contenues dans la série des moyennes :
(√5+1)/2 = θ; (θ+1)/2 = √e-1, (√e-1 +1)/2 = tau-1, ((tau-1)+1)/2 = √tau-1,
que formule l’équation : (N + 1)/2 = n.
De l’équation des moyennes : (N + 1)/2 = n, se déduisent les calculs de N = 2n – 1,
N – 1 = 2 (n – 1),
n – 1 = (N-1)/2 = N – n, etc.,
qui nous permettent de « lire » dans les quatre lieux : le temps et la durée, l’étendue et l’espace, mais aussi d’établir les différentes valeurs des diverses unités.
L’application aux quatre lieux –
A – n est plus petit que N :
1) dans la durée, n représente toujours un moment vécu.
Par exemple, √(e-1) quand N = θ
2) dans le Temps, n représente toujours une orbite à venir. Par exemple, n = 6 quand N = 11.
Dans la durée, le sentiment qui régit le calcul est le souvenir et la réalité qu’il mesure est le rejet; dans le Temps, la réalité que formule le calcul est le projet et le sentiment qui l’inspire est l’espoir.
B – n est plus que N :
1) dans l’étendue, n précède N, c’est-à-dire que j’anticipe toujours sur l’objet. Par exemple, si N (l’état actuel) égale 0,5 ou 1/2, n = (0,5 = 1)/2 = 0,75.
A partir de N = 8:10, n est conçu comme l’unité moins son inverse : (q-1)/q. Par exemple n = (0,8 + 1)/2 = (10-1)/10 = 0,9
2) dans l’Espace, n suit N, graphiquement, c’est-à-dire que je mesure toujours l’advenu. Par exemple, si N = -0,2, n = 0,4 :
Pour n = 0, N = 2 X 0 – 1 = -1.
Pour N = 0, n = 1/2.
Les trois unités – Nous avons vu que l’unité absolue ou quantique est donnée par l’équation : (q X 1)/q = 1.
L’équation demeure exacte si je pose : nq au lieu de q : nq X 1/nq = 1,
et d’une manière plus générale, pour toute formulation du type : N/n X n/N = 1.
Dans cette acception, l’unité quantique est indépendante des sens de la lecture (dans l’étendue) et du délit de vivre (dans la durée). Elle égale toujours 1.
Pratiquement, toutefois, dans l’actuel ou le relatif, ce calcul n’est jamais effectué. Car l’unité relative ou actualisée Ur doit être saisie comme la succession (la somme) d’une certaine lecture du cycle en soi et de la lecture de sa durée vécue. C’est-à-dire, comme la somme d’une certaine surface cyclique et d’une certaine surface vécue. Soit, selon le théorème de Pythagore :
D² = C’² + C »²,
ou selon l’équation d’Einstein, qui l’applique au temps :
t² = s² + x².
Nous aurons : 1² = √1/N² + √(n-1)²
ou : 1 = 1/N + (n – 1).
Pour N plus grand que 2, 1/N est moins grand qu’1/2, n est plus grand que 3/2 et l’unité relative est plus grande que l’unité : sous le nom d’unité aléatoire, elle fera l’objet d’un 3ème calcul.
Si N = 2, 1/N = 0,5, n = 1,5, n-1 = 0,5, 1 = 0,5 +0,5 = 1.
Si N = θ, 1/N = θ-1, n = √e-1, n-1 = 0,309, 1 = 0,618 + 0,309 = 0,917.
Si N = 1,5, 1/N = 0,66, n = 1,25, n-1 = 0,25, 1 = 0,66 + 0,25 = 0,91.
Si N = √e-1, 1/N = 0,763, n = tau-1, n-1 = 0,154, 1 = 0,763 + 0,154 = 0,917.
Si N = tau-1, 1/N = 0,866, n = √tau-1, n-1 = 0,077, 1 = 0,866 + 0,077 = 0,943.
Si N = 1, 1/N = 1, n = 1, n-1 = 0, 1 = 1 +0 = 1.
Il y a contraction de l’unité relative de n-1 = 0 à n-1 = 2/12 = 1/4, et dilatation de Ur de n-1 = 3/12 à n-1 = 6/12 = 1/2.
Cela se vérifie par la contraction du cycle circadien entre les équinoxes et les solstices, ou celle de la phase lunaire sur 6 940 jours. Je l’ai longuement vérifié dans l’ère précessionnelle de 2 160 ans, qui peut se réduire jusqu’à 1 980 ans (dans les 11/12 de l’ère) ou plus précisément jusqu’à 2 160 X 0,91 = 1 976 ans, comme on le vérifie par l’écart entre la réforme d’Esdras, réformatrice du Bélier : -432, et le concile de Trente, réformateur du Poisson : 1545 : 1 977 ans.
Cette contraction était connue d’Ezéchiel et de Platon, qui la situaient à 390 ans et 354 ans de la fin de l’ère; elle est reconsidérée en physique subatomique, sous le nom de précession de Larmor, aux 6/10 de la durée périodique (au 1/2) de la particule : le point de résonance où l’électron émet un photon de lumière[1], ainsi que, d’ailleurs, par la macrobiologie, aux 3/5 de la double hélice, où une certaine régularité se reconstitue.
Comme le Yi King, Platon figurait le renversement précessionnel par les deux cercles du Même et de l’Autre, et c’est aussi par la double rotation de la particule que la physique nucléaire le figure aujourd’hui, en admettant une perte d’énergie/masse et une réduction de fréquence quand l’électron inverse son mouvement, de l’éloignement au rapprochement du noyau.
Lorsque, artificiellement, on recharge la particule, elle s’éloigne donc du noyau; et c’est ce qui se passe aussi, à l’échelle macroscopique, dans ces périodes d’excitation (rationalistes/matérialistes) qui achèvent l’ère précessionnelle. Car, accroissant son énergie et sa fréquence, la particule – ou l’entité – n’accélère que son entropie et ne rapproche que sa fin (ou ionisation).
Mais quel feu d’artifices!
Quant à la troisième unité, il ne semble pas que son calcul puisse être aussi simple. Qu’il s’agisse de la survie de la matière dans l’Espace ou de l’avènement de la forme dans le Temps, il apparaît que cette forme ne peut être que vide ou de masse nulle et cette matière inlocalisable.
Puisque la vitesse est fonction de la masse/énergie, ou à l’inverse, comme on le vérifie par l’augmentation démesurée de la masse du méson à l’approche de la vitesse de la lumière, une forme sans masse se présente comme inerte ou sa quantité de mouvements comme hasardeuse, incohérente.
Puisque un objet qu’on ne peut localiser est, par définition, indiscernable, une matière sans forme ne peut être qu’invisible.
Dans la mesure où je définis toute unité, quantique ou actualisée, comme une quantité de mouvements localisable, un être non localisable (la substance spatiale) ou non cohérent (la forme temporelle) ne peut être que dépourvu d’unité.
Néanmoins, j’ai amis que quelque chose existe, qui précède l’apparence dans l’étendue et qui succède à la durée du cycle. Car, si cette chose n’existait pas, je ne vois pas d’où naîtrait le cycle et ce que deviendrait l’énergie/masse qui l’anime.
Autrement dit, je sais que le temps-trottoir des apparences n’est qu’une partie ou un état d’un autre mouvement (que j’imagine comme circulaire) et que la durée-balançoire n’est que la somme ou le produit ou la puissance d’une infinité d’autres balançoires (d’une multitude de danses corpusculaires).
Puisque l’unité quantique n’est que le produit de l’étendue par de la durée, et l’unité relative la somme d’u état de cette étendue et d’un moment de cette durée [1/N + (N-n)], il faut qu’un certain rapport existe entre l’Espace et le Temps, tel que s’y révèle l’unité troisième, matériellement potentielle ou formellement imaginaire, que je nomme l’Unité aléatoire.
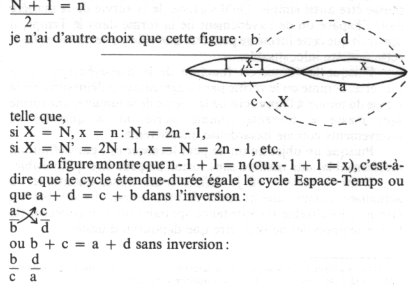
La symétrie asymétrique – Si je veux représenter géométriquement la formule :
1) Mais je sais aussi, en application de la formule des moyennes, que n-1 = (N-1)/2, c’est-à-dire que c est la moitié de b si c (la durée) égale n-1. Il se vérifie aisément que l’équation demeure exacte quelle que soit la valeur de c.
La somme a + d demeurant égale à la somme b + c et celle-ci égalant toujours 3c, il suit que a + d = 3c : la réduction de d (dans l’Espace) est proportionnelle à l’augmentation de a (dans le Temps).
2) Cependant, toujours vérifiée, l’équation : n-1 = (N-1)/2 n’est applicable à l’équation : b + c = a +d = 3c que dans un cas particulier où n = 2(N = 3) :
2 +1 = 3 + 0 = 3.
C’est-à-dire que cette équation n’est qu’un cas particulier de l’équation plus générale : N = 2n – 1, selon laquelle (n-1) + 1 = n.
C’est-à-dire que l’étendue comme le Temps peut recouvrir le Tout spatial-temporel quand 1 = q = 12 = le Temps (12 e) moins l’étendue 12(e-1).
Analogiquement le jeu se jouera aussi bien avec les 12 tribus ou les 12 chevaliers ou les 12 pierres précieuses, astrologiquement avec les 12 signes, alchimiquement avec les 12 opérations, philosophiquement avec les 12 catégories, théologiquement avec les 12 imams ou les 12 avatars tamouls, etc.
Calendériquement, avec les 12 mois dans l’année ou les 12 fois 2 heures du jour, ou les 12 ères dans la Grande Année; mais aussi bien, dans le cercle de 360 degrés, avec les 360 jours annuels (12 mois), ou les 25 920 parties hébraïques dans le jour, les 9 331 200 parties dans l’année ou les 9 331 200 ans ( 25 920 X 360) du Grand Kalpa. Ou, même les 12 960 d’une demi-grande année ou les 129 600 = 360 au carré, etc.
Chronologiquement, le jeu ne sera pas si complexe, puisque :
a) en tenant compte de l’unité aléatoire, les unités s’ajoutent comme d’un nombre entier à l’autre : 3, 4, 5, etc.
b) sans tenir compte de l’unité aléatoire, la durée n’est que l’Espace = 1, l’étendue la durée + 1 et le Temps l’étendue + 1, et que, dans les deux cas :
l’étendue + la durée = le Temps + l’Espace,
l’étendue + la durée – l’espace = le Temps,
N, le moment ou l’état réel = 2n (la lecture que j’en fais) – 1 et la distance intellectuelle ou le degré de liberté N-n = n-1 = (N-1)/2.
Unique fondement mathématique de tous les calculs précédents, le degré de liberté N-n n’est que la période de l’inévitable écart (temporel ou spatial) entre le moment ou l’état réel et l’introuvable unité : N-1.
Ce degré de liberté (N-n) ne peut évidemment que croître à mesure que croît N-1, c’est-à-dire dans l’exercice de tout raisonnement causal, que celui-ci s’exerce dans l’étendue (n>N) ou dans la durée (n<N).
Au contraire, dans l’exercice du raisonnement non-causal, l’écart N-1 (et par suite l’écart N-n) tendront à s’annuler.
On donnera, comme exemple de raisonnement non-causal, toute mathématique symbolique, fondée sur des nombres constants, tels que le nombre 12 ou toutes les constantes des moyennes ou, d’une manière plus générale, toute constatation mathématique, très comparable à la constatation ludique des figures et des règles d’un jeu.
Q/(Q-5) – Dans ce premier exemple, la constatation est celle de la double série qui ordonne les moments de la durée :
a) la série des moyennes : √tau-1, tau-1, √e-1, θ jusqu’à e-1,
b) la série fractionnelle : 12/11, 12/10, 12/9, 12/8, 12/7.
On voit que chacun de ces nombres est recouvert par la formulation : Q/ (Q-5) :
√tau-1 = 69/64, θ-1 = 39/34, √e-1 = 21/16, e-1 = 17/5,
12/11 = 60/55, 12/10 = 30/25, 12/9 = 20/15, 12/8 = 15/10.
Nous dirons donc que, dans la durée d’un cycle (et de l’objet qui épouse ce cycle), la formulation Q/(Q-5) est prépondérante. Or, elle formule seulement la somme de l’unité quantique : Q/Q et de la fraction : 5/q, comme 12/7 = 7/7 + 5/7 = 1 + (N-1) si 12/7 = N.
Si Q/(Q-5) formule tous les moments de sa durée, cela signifie qu’à tout moment de sa durée, un corps quelconque est à la fin d’un cycle : N-1 se formule 5/q.
Les quatre cinquièmes – La constatation qui fonde le calcul est celle de la constance du rapport entre les puissances de 2 d’une part et la série des moyennes : N = 11 pour n = 6, N = 21 pour n = 11, N = 41 pour n = 21, etc.
En sorte que la lecture « apparentielle » du cycle, en ses 4/5, révèle la succession de la série des moyennes à l’infini.
Cherchant à comprendre la règle de ce jeu, je m’avisai de le jouer non plus à partir de l’unité quantique : 1, mais à partir de toute unité aléatoire : q.
La figure-clé des moyennes :
présente alors au plus simple le rapport : q = 1, n-q = 2, n = 3, N = 5,
tel que : q = N/5, n = 3n/5, n + q = 4N/5, et (n + q)/N = 4/5.
Or, ce rapport demeure constant pour toutes les applications mathématiques, ésotériques et scientifiques de la figure :
Pour N = 360° (le cercle), q = 72°, n = 216°, n + q = 288/360 aux 4/5,
N = 2 160 ans (l’ère), q = 432, n = 1 296, n + q = 1 728/2 160,
N = 9 331 200 (vibrations du césium ou respirations, etc.), q = 1 886 240, n = 5 598 720, n + q = 7 464 960, aux 4/5 de 9 331 200.
Enfin, ces 4/5 se présentent toujours comme une puissance de 12 (ou son multiple) : 228 = 2 X 12²; 1 728 = 12³; 7 464 960 = 30 X 12⁵.
Pour la succession des nombres entiers :
si x = 2, n + q = 4N/5 = 24/5, N = 6 = 2n-q, N + q = 4,8 q = 1,2 n = 3,6
x = 3, n + q = 4N/5 = 44/5, N = 11, N + q = 8,8 q = 2,2 n = 6,6
x = 4, n + q = 16,8 N =21, q = 4,2 n = 12,6
x = 5, n + q = = 32,8 N = 41, q = 8,2 n = 24,6, etc.
Dans l’étendue ou dans le cycle, à partir de l’unité quantique 1, et dans le Temps ou dans les cycles supérieurs, à partir de l’unité aléatoire q, la fraction 4/5 se présente comme constante. Elle établit, hors tout degré de liberté, l’égalité des deux rapports : 2 puissance x/N-1 et (n +q)/N, dans le contenu du cycle, son état, N-1, d’où se déduit le degré de liberté N-n = (N-1)/2, et dans les contenants du cycle à l’infini.
Les niveaux – J’ai pu considérer le dénombrement :
l’une est un cas particulier de l’autre, bien que l’égalité : a + d = b + c puisse être préservée, si d = c.
Il me faut considérer les trois formulations : c/d = 1/0 = ∞, c = d +1 et c = d comme trois niveaux de la perception cyclique, selon que le rapport c/d est l’infini, le reste c-d l’unité, et l’Espace d l’équivalent de la durée c.
Au niveau du rapport, l’étendue (b) est le double de la durée et le Temps (a) le triple de celle-ci,
au niveau du reste, l’étendue est la somme : durée plus unité, et le Temps est la somme : étendue plus unité,
au niveau de l’équivalence, durée = Espace, l’étendue et le Temps sont équivalents de même.
Il demeure que, dans cette triple lecture, l’Espace est tantôt la durée moins l’unité, tantôt 0, tantôt égal à la durée. Ce ne peut être simultanément.
Si d = c-1, d = 0 quand c = 1.
Il faut donc admettre que d = c au-delà de d = 0. C’est-à-dire que l’Espace devient une autre durée au-delà de a/d = 2,998.10¹⁰.
La seule équation qui demeure vérifiable à travers les trois niveaux est a + d = b + c ou l’Espace + le Temps = la durée + l’étendue. Mais je ne la vérifie que dans le simultané.
De ce fait, la figure ci-dessus est ou bien théoriquement fausse ou bien pratiquement inutilisable. Quand, dans deux quelconques des quatre lieux, les trois niveaux se présentent comme successifs en chaque lieu (et concordants d’un lieu à l’autre), ils se présentent comme simultanés dans les autres lieux.
Or, si je ne puis approcher l’Etre que dans cette contradiction fondamentale, je ne le dirai absolument (à la fois et successivement dans son retour et ses mutations) que par l’hypothèse des 12 ( 3 X 4) : conditionnements, conservations, catégories, symboles, lois, archétypes, démons, dieux, etc., selon le douzième choisi.
Les nominations hors du cycle – Nous avons vu qu’en effet, les 4/5 du cycle se présentent toujours comme un multiple des 12 nominations : 12, 144, 1 728, etc. D’où le problème : comment se présente hors de soi (dans le Temps et dans l’Espace) une telle étendue-durée?
Le cycle en soi, comporte comme sommation le nombre e-1 = 12/7.
Sa lecture aux 4/5 sera les 4/5 de (e-1) = 1,37456 + 7/5.
Si N = 1,37546, 1/n = 0,7275, ou e-2 à 0,01 près.
Cette lecture exclut l’unité quantique : e-2 = (e-1)-1 et le rapport étendue/espace-temps devient :
pour sauvegarder l’équivalence : étendue + durée = Espace + Temps.
J’aurai créé une forme vide (qui ne contient plus l’Unité) aux 4/5 de la lecture du cycle et, dans le Temps, aux (2e-3 = 12/5) de l’unité quantique. Si la lecture est aux 4/5 de l’unité cyclique, la forme vide est aux 7/5 (12/5 – 5/5) de l’unité.
Une telle forme vide sera le cycle chinois où les 5 saisons sont lues 4 dans le cadre des 7 (ou les 15 lunaisons, 12 en 21). Elle reporte le cycle de 180 ans en 144 ans sur 252 ans ou le cycle « précessionnel » en 1 728 sur 3 024 ans, etc.
Ce n’est rien que l’application de l’équivalence :
1 + 2(e-2) = (e-1) + (e-2) = 2e – 3?
l’unité + la nomination aux 4/5 = le cycle + sa durée entropique.
Jean-Charles Pichon
[1] A 4/10 de la fin de sa période, la particule est aux 2/10 de la fin de son unité-vie. 2/10 = 432/2 160. Les 8/10 ou 4/5 de son unité-vie sont alors vécus.