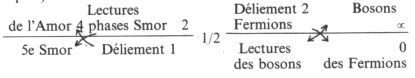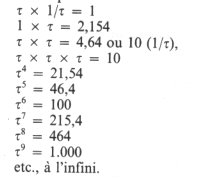6 – LES DIVERSITES DE L’UNITE

6

LES DIVERSITES DE L’UNITE

 

Pour tenter de mieux comprendre les Machines, reprenons la démonstration au point où nous l’avons laissée : la coexistence d’un degré de liberté quantique, que nombrera, au moindre degré, l’inverse du quantum choisi, et d’un degré de liberté aléatoire, déterminé, à tout moment, par l’alternance propre au cycle.

Ici encore, je pourrai prétendre dans les deux cas :

à) soit que le problème n’existe pas : l’unité d’un cycle est ce cycle même. Le jour est Un au terme des 24 heures, l’année au terme des 365,25 jours, telle vie de 65 ans au terme des 65 ans,

b) soit que le problème est insoluble, car je ne peux déterminer l’unité aléatoire d’un cycle qu’en fonction de la lecture que j’en fais, c’est-à-dire de la signification que je donne au nombre 1 : le maximum du possible (la pleine lune, le maximum d’activité solaire, ma pleine maturité) ou son minimum (la nouvelle lune, le minimum d’activité solaire, l’unité primaire du fœtus) ou n’importe quelle phase entre ces deux extrêmes : le Jaune est une Unité, tout comme la note La, l’enfant que je fus était Un, comme l’adolescent qui suivit.

Mais, ces deux délires écartés, on voit que le problème demeure. Plus exactement, il se dialectise : en seuils de l’Unité d’une part, en unité de chaque seuil de l’autre.

Les seuils de l’Unité

Je peux concevoir l’unité comme une totalité (en tant qu’unité finale) : les 24 heures du jour, les 30 jours du mois. Je la définirai dès lors comme « quantique » et l’identifierai au cycle même.

Ou je peux la concevoir comme un point d’origine, la cause d’une série d’effets ou le premier nombre d’une série mathématique quelconque, par exemple.

Examinons l’une et l’autre.

a) Je ne peux formuler l’unité quantique qu’à un degré de liberté près : ni le jour n’a vraiment 24 heures, ni le mois 30 jours, ni l’année 360 jours, etc. Nous avons vu que, dans la plupart des cas, ce degré de liberté ne peut être moindre que l’inverse du quantum choisi : s’il est d’un jour dans le mois de 30 jours, il sera d’un mois dans l’année lunaire de 12 mois lunaires (328 jours) ou de 12 mois solaire (365,25 jours).

Si je commets l’erreur de confondre l’unité réelle avec l’unité quantique moins ce degré de liberté : 1 – 1/q = (q – 1)/q, je découvrirai que (q-1)/q comporte également un degré de liberté.

¨Par exemple que les 365,25 jours ne correspondent pas vraiment à 365,25 tours de la terre sur elle-même, ou que le mois lunaire n’est pas de 28 jours mais de 27,33 jours, etc.

Mathématiquement, si je pose : q = 12, q – 1/q = 11/12.

Mais 11/12 comporte également son degré de liberté, au 1/11.

11/12 – 1/11 = 9/11 + 1/132 ou 9/11 + 1/(12² – 12),

ou :

11/12 – 1/11 = 10/12 – 1/132.

Je puis donc écrire :

9/11 + 2/132 = 10/12.

En poursuivant, je démontrerai que, de même, les degrés de liberté possibles, à l’infini, joueront de : x-3/x, x-4/x, x-5/x, etc.

C’est-à-dire que leur succession s’inscrit dans la série des « degrés de lecture » possibles : 11/12, 10/12, 9/12, 8/12, etc., définis comme les « seuils de lecture » au paragraphe suivant.

b) Différemment, si je ne considère pas l’unité comme une « lecture », je devrai la considérer comme une cause de déliement ou de « délit » (de sa propre durée), c’est-à-dire comme le premier terme d’une série quelconque d’inverses, telle que la série des factorielles inverses : 1 + 1/2 + 1/6 + 1/24 + … à l’infini = e-1.

Mais on voit qu’ici, de même, l’unité ne sera pas formulée directement. Elle ne sera que le reste d’une des deux soustractions :

soit : e – (e-1) ou 19/7 – 12/7 = 7/7,

soit : (e-1) – (e-2) ou 12/7 – 5/7 = 7/7.

Par exemple, si je donne à la durée e-1 la valeur de l’ère précessionnelle : 2 160 ans, aux 12/7 de l’unité, l’unité de l’ère est le « temps » apocalyptique : 2 160 – 900 = 1 260 ans.

La valeur de la constante « e » est alors : 2 160 + 1 260 = 3 420.

Si la durée d’une vie est 60 ans, l’unité de cette vie a porté sur les 7/12 de cette durée ou 7 X 5 ans = 35 ans et « e » vaut 60 + 35 = 95 ans; quant à savoir à quel moment de cette vie les 95 ans possibles ont commencé de se réduire en 60 ans de durée effective, ce calcul-là échappe aux nombres.

En effet, la vie de cet individu a de fait duré les 60 ans, et son unité même (35 ans) se déduit de cette seule durée. C’est-à-dire que, progressivement, au cours des 60 ans, son unité s’est réduite des 7/12 de 95 ans aux 7/12 de 60 ans.

Mais, si son unité « de finalité » avait été les 7/12 de 95, quelque 40 ans, sa « durée » aurait été autre : les 12/7 de 40, quelque 68,5 ans. De cette durée se serait déduite une unité différente, etc. à l’infini.

Dès l’instant qu’on ne mesure la durée d’une vie qu’au moment de la mort, l’unité du vivant n’apparaît qu’à sa mort. Sur le squelette seulement se fonde la renommée.

On dira que les cycles ou les « formes du temps » échappent au paradoxe : d’une heure de 60′, d’un jour de 24 heures, d’un mois de 30 jours, je pourrai déduire à coup sûr l’unité de cette heure, de ce jour, de ce mois.

Vingt observations nous ont révélé qu’il n’en était rien. Car, si je définis cette unité par les 7/12 du cycle, je ne mesure qu’un maximum dans le jeu maximum 7/5 qui ne détermine qu’exceptionnellement, comme d’ailleurs 6/6 ou 5/7, l’alternance vécue du cycle : refroidissement/réchauffement, croissance/décroissance, ordre/désordre, etc.

Or, la saison ou le quartier, qui se présente alors comme la période de l’unité (au 1/2), offre un degré de liberté non moindre que celui qu’offre la « période » de l’unité vivante.

On le vérifie aisément par les exemples précédemment étudiés : la « période » de l’unité a.s. n’est que la moyenne entre les deux unités possibles :

(5 + 7)/2 = 6 ans sur 12 (+ ou -);

la période de l’année (deux saisons) n’est qu’une telle moyenne :

(5 + 7)/2 = 6 mois (+ ou -);

la période de la lunaison (deux quartiers) également :

(12,5 + 17,5)/2 = 15 jours sur le mois.

De même, la période d’une unité vivante (un homme) sera, dans l’exemple donné :

soit

(25 ans + 35 ans)/2 = 30 ans, « période » d’une vie de 60 ans,

soit

(35 ans + 42 ans)/2 = 38, 5 ans, « période » d’une vie de 77 ans.

Mais le calcul précis en demeurera incertain aussi longtemps que le sujet ne sera pas mort, révélant de la sorte s’il a vécu 60 ou 77 ans.

La réflexion la plus courte suggère donc que la seule distinction réelle entre une vie qui se vit – la mienne – et un cycle planétaire quelconque réside en cela que le second ne cesse d’être « vécu » lorsque ma vie ne l’a pas été.

Au contraire, les phases purement quantiques d’une vie non vécue, par exemple les 7 phases de 7 ans d’origine chaldéenne ou les « 4 âges » de la croyance contemporaine offrent des analogies parfaites avec les phases calendériques déduites des cycles planétaires : saisons de l’année, mois de la saison, jours du quartier lunaire ou de la semaine de 7 jours, etc.

Car, dans tous les cas, la moyenne des deux « probabilités d’unité » formule précisément la moitié de l’onde qu’est aussi le cycle et que constituent l’augmentation et la réduction, le refroidissement et le réchauffement, l’assimilation et la désassimilation, ou à l’inverse.

Cette probabilité d’unité n’est elle-même que dialectique, constituée de deux figures (dans l’analemme) dont l’une croît quand l’autre décroît, ou de deux nombres dont l’un est l’inverse de l’autre, comme 5/7 et 7/5.

Je dis ce principe universel, puisqu’il se vérifie dans les cycles, plus réduits, que circonscrivent les rythmes biorythmiques, cardiaques, de la respiration ou celui, qu’on commence de mieux connaître, que circonscrit le rythme du sommeil et de la veille.

La veille et le sommeil – Si je choisis ce rythme pour exemple, c’est que, de plus en plus, on le considère comme déterminant dans la vie de l’individu. Il se pourrait qu’à la limite, il se répercute sur des rythmes aussi divers que ceux de la pression artérielle, du rythme respiratoire, de la résistance électrique de la peau, du contenu du sang en globules, en sels minéraux, en hormones… On lui associe déjà certains rythmes bien déterminés, comme celui de l’activité et de la passivité, au plan psychologique, ou celui de la sécrétion de la glande surrénale, au plan somatique, etc.

Mais c’est aussi que, communément, on le tient pour l’un des plus simples qui soit, en le reliant étroitement au rythme circadien : refroidissement/réchauffement, sensible dans les 24 heures.

De fait, il se relie bien à l’échelle des températures, mais thermométriques et non pas barométriques : dans le cycle individuel et non dans un cycle cosmique.

Réduit à sa plus grande simplicité, le principe semble être ici que le sujet se réveille inévitablement lorsqu’il atteint au point de température maximale (quelque 37°). En effet, si le sujet s’endort pendant la phase descendante de température (de 37° à 36°), son sommeil sera beaucoup plus long que s’il s’endort pendant la phase ascendante de température (de 36° à 37°).

Dans le second cas, il pourra n’être que de 7 à 8 heures; dans le premier, sa durée pourra atteindre les 14,5 ou 15 heures.

Relié au rythme de la température individuelle, il suit que le cycle veille/sommeil ne l’est pas au cycle circadien. Chez un sujet libre, que le rythme social ne conditionne pas, il n’est même pas contenu dans les 24 heures. Des expériences ont montré qu’isolé du contexte social, un homme pourrait vivre un rythme circonscrit par les 50 heures (quelque 2,23 jours).

Ce nombre est important car, dans la plupart des cas, déconditionné puis reconditionné, le sujet ne se réadapte au rythme social qu’au terme de 24 jours, et « l’accord » dure quelque 2,3 jours.

24 + 2,3 = 26,4 jours et

26,4/13 = 2,23 jours, dont la « période » est 2,23/2 = 1,15 jour ou 27,6 heures.

27,6/12 = 2,3 heures.

Partagé en 12 phases, le temps de 27,6 donne : 11,5 h aux 5/12 et 16,1 h aux 7/12, c’est-à-dire d’une part la moyenne entre le sommeil court et le sommeil long, d’autre part la moyenne entre la veille longue et la veille courte chez le même sujet.

L’étude du sommeil lui-même (dit « normal ») ne donne pas des résultats moins significatifs. On y distingue :

1) le sommeil proprement dit, SMOR (sans mouvements oculaires rapides),

2) le temps de rêve ou d’activité extraveille, l’AMOR (avec mouvements oculaires rapides).

Le SMOR comporte normalement 5 cycles de 90′ chacun : a) quelques minutes de passage de la veille au sommeil, b) de 10′ à 30′ de « sommeil confirmé », c) une phase Delta, à ondes lentes, dite de « sommeil profond », qui se réduit de cycle en cycle sous l’influence du sommeil AMOR.

A l’inverse, lors du 1^er cycle, la phase Delta s’achève par une phase réduite de sommeil AMOR, assimilée à une première période d’activité mentale (ou de rêve), très brève (de 1′ à 5′).

Dans les cycles suivants, cette phase AMOR recouvre le 1/4, puis le 1/3, puis le 1/2 de la phase Delta, pour atteindre l’heure (60′) dans le dernier cycle.

Si le sujet dort régulièrement moins de 450′ (90′ X 5), il en vient à réduire le rythme des phases jusqu’à ce qu’il ait atteint un autre point d’équilibre (la phase AMOR préservée). Si l’on rend impossible l’avènement de cette phase, en réveillant le sujet dès les premiers mouvements oculaires rapides, le sujet se déséquilibre : la poursuite de l’expérience le détruit.

Les degrés de liberté notables ici sont donc de véritables processus d’adaptation ou de réadaptation du sujet au cycle calendérique qu’on lui impose.

D’autre part, l’alternance veille/sommeil, recouvrant l’alternance chaud/froid (de l’infrarouge à l’ultraviolet) ou froid/chaud, dans le sens inverse, se présente comme rigoureusement analogique aux alternances : réchauffement/refroidissement, activité/passivité, organisation/désorganisation, notables en tous les cycles et qui elles-mêmes correspondent à l’alternance : accroissement/réduction du degré de liberté.

Etudier un cycle (quelconque) en soi, ce n’est rien d’autre qu’étudier les phases de croissance et de décroissance de ses degrés de liberté. Comme si, dans l’Univers entier – ou dans l’Etre en soi – l’irrégularité cyclique ne tendait jamais qu’à rejoindre une régularité quantique (de quantum 12 ou d’un multiple de 12 ou d’une puissance de 12, etc.).

Mais, précisément, aucune étude d’un cycle « vivant » (d’un animal, d’un homme ou d’un astre) ne révèle l’unité du vivant, en raison de la permanence du degré de liberté le plus court : 1/q, d’une part, et, d’autre part, de la variabilité des degrés de liberté d’alternance, liés à la « durée » du vivant.

A la limite, l’étude de l’introuvable Unité semble devoir passer par l’étude des seuils qu’elle ne cesse de franchir, depuis sa formation jusqu’à sa destruction.

L’étude de la veille et du sommeil, venant après celle des cycles calendériques, montre que ce « seuil » peut être simplement une limitation de la durée (par exemple, du sommeil au point de température maximale) ou une limitation de la série quantique (5 cycles de 90′) ou la formulation d’une nécessité finale, d’une véritable finalité (la période AMOR triomphante). Mais on voit que chaque seuil modifie de fait la notion même – et la mesure – de l’Unité en soi : l’unité de température n’est pas l’unité quantique, aucune des deux n’est l’unité de finalité que pourrait être l’unité de l’AMOR chez tel individu déterminé.

A la limite ainsi, l’introuvable Unité semble se diversifier en un certain nombre de « figures » ou de « nominations », qui la définissent en effet diversement. Dans l’exemple choisi : comme « unité causale », « unité quantique » et unité révélatrice de sa finalité ou de sa vocation, qu’on pourrait appeler « finale ».

Le jeu mathématique – Nous voyons cependant, par l’exemple donné, que cette triplicité de l’Unité n’est pas choisie pour fondement des divers calculs. Un choix, ici, prime tous les autres : celui de l’Unité au 1/2 ou la période.

Le rythme global ou unitaire est partagé entre le sommeil et la veille. Puis, le temps de sommeil en AMOR et SMOR. Nous savons d’avance que l’étude du temps de veille, moins avancée, se portera sur les concepts périodiques de passivité et d’activité, dont il se pourrait qu’une observation plus précise modifie les nominations en : accélération/ralentissement, etc.

Pour ne traiter que des résultats rendus publics, un principe s’en dégage, de « complexité », tel que ni l’AMOR ni le SMOR ne se présentent comme observables en soi ou sans tenir compte de l’autre cycle.

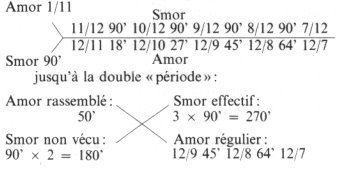
a) le 1^er cycle SMOR, de 90′, se situe hors de la phase AMOR; mais le 5^ème cycle de 90′ est comme « envahi », aux 5/7 par la phase AMOR;

b) les phases Delta (SMOR) se réduisent de cycle en cycle, tandis que les temps AMOR augmentent, de cycle en cycle, dans le rythme approximatif :

1/11, 2/10, 3/9, 4/8, 5/7 des 90′,

ou : moins de 8′, moins de 18′, moins de 27′, moins de 45′, moins de 64′.

Soit, en y adjoignant l’unité quantique (90′ ici) :

11/11 + 1/11 = 12/11,

10/10 + 2/10 = 12/10,

9/9 + 3/9 = 12/9,

8/8 + 4/8 = 12/8,

7/7 + 5/7 = 12/7,

alors que les cycles SMOR jouent de fractions égales de temps, au 1/q (1/12 si q = 12).

Le problème est que, d’une part, le nombre SMOR : 5 X 90′ = 450′ n’est pas constant : il peut n’être pas atteint dans le cas d’un sommeil très court, alors que le nombre AMOR, quelque 162′ : 8 + 18 + 17 + 45 + 64 = 162′ tend à l’être dans tous les cas.

Par exemple, si le sommeil ne dépasse pas les 270′ (avec un retard de 180′) la phase AMOR sera de 50′ dès le premier cycle, donnant un total de : 50′ + 45′ + 64′ = 159′.

Mais c’est alors le double jeu des deux rythmes SMOR et AMOR qui se trouve modifié, depuis le plus petit degré de liberté (1/q) :

La conjugaison des deux Unités : causale (le le sommeil SMOR) et finale (le sommeil AMOR) ne peut être réalisée que par l’utilisation d’une troisième Unité, quantique.

Mais cette conjugaison ne s’accomplit que dans le cadre de la double période ou des quatre « lieux ».

Le quantum à choisir ne peut donc être que : 3 X 4 = 12.

(1) Par exemple, dans le « temps » que délimite la constante de Planck, un proton passe par 11 métamorphoses avant de se retrouver le proton d’origine en son 12^ème état.

Il ne s’agit là cependant que d’une connaissance pratique ou expérimentale, comme celle qui nombre les phases AMOR aux 1/11, 2/10, 3/9, 4/8 et 5/7 de 12/11, 12/10, 12/9, 12/8 et 12/7 de 90′ dans un « jour » veille/sommeil de 12 X 90′ = 18 heures et un sommeil de 5 X 90′ = 7,5 heures ou 450′.

Ou comme celle qui situe les couleurs entre 5/12 et 9/12 du micron, par l’étude de leurs longueurs d’onde, et les sons musicaux entre 1 = 12/12 et 2 = 12/6 dans une octave donnée, en fonction de leurs fréquences;

ou comme celle qui donne la constante (e-1) = 12/7 pour sommation de la série des factorielles inverses et pour limite de toute durée, etc.

Ces numérations ne nous éclairent pas sur la « nature » de l’alternance SMOR/AMOR, ni sur la théorie de l’inversion longueurs d’onde/fréquences, ni même sur le rapport : périodicité/durée d’un corps radioactif.

Nous voyons seulement que, dans tous ces cas, et en bien d’autres que je pourrais citer (biorythmes, analemme), le problème demeure, irrésolu, de l’Unité en soi.

C’est toujours le problème posé dès les premières pages de ce livre : un objet m’étant donné, dirai-je que son unité circonscrit les parties qui le composent (q) ou le considérerai-je lui-même comme la partie quantique d’une autre chose (le bâton comme une branche d’arbre, le fragment de bâton comme un nouveau bâton) au 1/q de quelque totalité autre?

Si le quantum est le nombre 12, dirai-je que l’Unité est l’ensemble de ces 12 ou qu’elle n’en est que le 1/12?

Bien évidemment, elle est à la fois le 1/12 de 12 et 12 fois son 1/12 propre, c’est-à-dire que 1 égale toujours : 1/q X q = q/q.

Il peut arriver cependant qu’expérimentalement et numériquement, l’unité se présente aussi comme la moyenne des deux grandeurs, c’est-à-dire que :

(q + 1)/2 = 1 ou √1.

C’est le cas si q = 1.

Ce l’est aussi quand q = x plus petit que 12/11 (ou 1,09 entre h barré = 1,054 et tau – 1 = 1,154).

De ce nombre jusqu’à l’infini (sans atteindre le nombre 1) : (x + 1)/2 = √x.

Ce l’est enfin quand q = x plus grand que 11/12, entre 1/h barré et 1/tau – 1).

Depuis 1 (indéfini) jusqu’à ce nombre : 2/(x + 1) = 1/√x.

En réduisant à la fraction 12/11 (1,09) les constantes qui limitent l’application de l’équation unitaire (1,054 et 1,154), je dois donc présenter cette moyenne comme un seuil de déliement, ou de délit, si l’observateur n’est pas innocent de la modification en cause, car il ne la lit pas sans la vivre.

Mais l’équation unitaire atteste que le seuil de déliement 12/11 n’est pas une autre réalité que le seuil de lecture 11/12, puisque l’unité (√1 = 1) se prend indifféremment de l’un à l’autre.

Je peux donc dire que 11/12 est la lecture de 12/11 et ne peux m’interdire de me demander s’il n’en irait pas de même en tous les degrés de lecture (comme Newton s’est demandé s’il n’existait pas une correspondance continue entre la « gamme » des couleurs, dans le lisible, et la gamme des sons dans la durée ou dans le rapport longueur d’onde/temps).

Le plus simple raisonnement démontre :

a) qu’une telle correspondance existe,

b) qu’elle n’est pas celle qu’on peut d’abord imaginer.

En effet, toute lecture joue des deux unités : quantique et aléatoire.

Quantique, elle entraîne un degré de liberté déterminé par la position du cycle comme contenant ou contenu, c’est-à-dire sa numération : par exemple, 12 fois 1/12 ou le 1/12 de 12, si le nombre quantique est 12.

Aléatoire, elle apparaît comme liée à de certaines constantes (, e-1) ou aux fractions équivalentes : 12/11, 12/7, qui se présentent comme des seuils, au-delà desquels l’unité même du cycle doit être modifiée, et sa formulation mathématique déduite d’une nouvelle constante ou d’un nouveau facteur.

Or, ces seuils ne sont plus seulement « seuils de lecture » mais seuils d’accroissement ou de décroissance, de remembrement ou de démembrement, de convergence ou de divergence, de diastole ou de systole, etc., c’est-à-dire d’alternance, tels que, tantôt les « deux cercles » de Platon semblent s’y défaire en un analemme de moins en moins définissable, tantôt la figure – informelle en sa limite – tend à se reconstituer dans la figure lisible et mesurable.

Tout cycle : a) contient en soi une telle alternance, qui le constitue; b) est lui-même contenu dans une telle alternance, dont il n’est en somme qu’une des phases ou l’un des facteurs quantiques, à un moment donné de son évolution.

Mais, si quelque unité quantique me permet toujours de déterminer, avec un degré de liberté plus ou moins grand, le moment donné de l’évolution du cycle (sa « quantité de mouvements ») et donc ses seuils de déliement ou de reliement, il faut qu’à l’inverse, seule quelque unité aléatoire se déduise des seuils de lecture du cycle (selon le quantum choisi).

C’est alors le « seuil de lecture » qui apparaît comme relatif ou contingent, le « seuil de déliement » qui apparaît comme absolu ou nécessaire. C’est le premier qui exclut la notion de constante et le second qui l’exige, inversant de fait toute concordance entre la série – fractionnelle – des lectures et la série – factorielle – des vitesses et des masses, des « quantités de mouvements » et des phases d’alternance, entre autres.

Dépassement du seuil

Il convient dès l’abord de s’entendre sur le mot.

Car l’ésotériste et le pragmatiste, trop souvent, ne connaissent – ou n’avouent – que ces deux seuils (0) et l’infini (∞), infranchissables tous les deux.

L’étude de l’unité – inaccessible – nous a révélé en elle un seuil non moins absolu : elle ne peut être qu’approchée ou dépassée (évitée?) mais jamais atteinte.

Puis, des études aussi diverses que celle du « spin » électronique ou des fonctions (différentielles ou intégrales) révèlent un autre couple de seuils, que de nombreuses séries convergentes mettent également en évidence, telles que les séries fuchsiennes de Poincaré : le 1/2 et le 2.

Ce sont là, en quelque sorte, les « seuils absolus », qui correspondent d’ailleurs aux trois énigmes de l’Etre : l’inexistence de l’unité, l’inversion de l’appareil, l’éloignement illimité du seuil (le néant ou l’infini).

Mais il est un seuil d’une autre nature et qu’on pourrait dire insituable ou incessant. Il apparaît d’abord comme multiforme ou innombrable. Je lui ai donné pourtant ces deux formes : le seuil de lecture et le seuil de déliement. Puis, je crois être parvenu à les contenir toutes deux dans la série :

11/12, 10/12, 9/12, 8/12, 7/12, 6/12, 5/12, 4/12, 3/12, 2/12, 1/12 et son inverse, de 0 à 1 la première, de 1 à ∞ l’autre.

 

Les seuils de lecture – En effet, un quantum étant choisi (ici le 12), il est clair que les lectures du cycle ne sont pas en nombre infini.

Elles comporteront nécessairement un degré de liberté défini, soit au 1/q, soit aux 2/q, 3/q, 4/q, etc., jusqu’à (q/2)/q dans le lisible et en-deçà du 1/2 dans l’illisible.

Il apparaît alors que chaque nombre de la série au 1/12 retenue se présente comme le seuil d’une nouvelle série de lectures :

Non seulement les 11 nombres de la série 11/12, 10/12, 9/12… 1/12 contiennent toutes les lectures du type : (q-n)/q pour q inférieur à 12 et n inférieur à q, mais la série contient tous les passages d’une série de lectures à l’autre, sans l’intervention d’aucune inversion.

Dans la mesure, cependant, où cette lecture tolère un degré de liberté (n/q), elle entraîne la possibilité d’une lecture contraire, du type : (q + n)/q telle que la somme des deux lectures sera toujours :

[(q – n) + (q + n)]/q = 2q/q = 2,

et l’Unité, le 1/2 de cette somme (ou la moyenne entre (q-n)/q et (q+n)/q.

Par exemple : (7 + 5)/7 + (7 – 5)/7 = (12 + 2)/7 = 2.

Les seuils de déliement – Le  problème qu’ils posent est tout différent.

Soit le seuil : (e-1), sommation des factorielles inverses et limite de toute durée cyclique, que formule la fraction 12/7 (à 0,004 près). La lecture de son unité exige l’inversion de la fraction en 7/12 de la durée cyclique, et l’Unité se présente comme le produit : q X 1/q.

Dans l’ensemble (12 X 7)/(7 X 12) = 1.

Déduite d’un seuil de lecture, l’Unité se présente comme la moyenne du seuil et de son contraire, ou comme la moitié du double;

déduite d’un seuil de déliement, elle se présente comme le produit du seuil et de son inverse.

A la différence des seuils, qui n’exigent aucune inversion pour reconduire à l’Unité, tous les seuils de déliement exigent un tel renversement pour y reconduire.

Or, si tous les seuils de lecture se laissent ramener à la série 11/12, 10/12, 9/12… 1/12 (à l’exception près de 4/5 et de 5/7*), tous les seuils de déliement se laissent ramener à l’inverse de la série (ou à 7/5 et 5/4).

* Les multiples de 12 ne sont pas divisibles par 5 et par 7.

Pris comme de tels seuils, les sons harmoniques s’y laissent ramener : 12/10 est le nombre de Mi, à 0,05 près; 12/9 est le nombre de Fa, 12/8 le nombre de Sol, 12/6 ou 2 reconduit à l’octave supérieure.

12/11 = 1,09 limite assez précisément l’équation paradoxale :

(x + 1)/2 = √x,

12/7 = e -1, à la 3^ème décimale près, etc.

Différemment, le rapport 5/7 et son inverse se présentent comme des constantes utilisables dans l’étude du renversement interne, commun à tous les cycles définis : aux degrés de liberté près, nous l’avons vérifié dans le jeu des saisons effectives, dans le jeu des quartiers lunaires, dans le jeu de l’accroissement et de la réduction de l’activité solaire et, moins rigoureusement, dans le jeu systole/diastole des cycles d’aspects planétaires. (1)

(1) Je traiterai plus loin du seuil de lecture aux 4/5 ou 8/10. Mais on notera que cette fraction n’est que le contraire du seuil de déliement 12/10, en jouant du degré de liberté aux 2/10. L’Unité quantique, moyenne, est alors 10/10 = 1.

Autant le partage d’un cycle en deux périodes égales (6/6) ne se rencontre qu’exceptionnellement, autant le partage 5/7 ou 7/5, s’y présente communément. Ce n’est jamais, d’ailleurs, que l’application la plus simple du degré de liberté du 1/12, telle que 6 + 6 se lit soit : (6 + 1) + (6 – 1), soit à l’inverse.

Les mêmes rapports ne sont pas autres que les 1 260/900 et 900/ 1 260 dans l’ère de 2 160 ans, que l’auteur de l’Apocalypse et Joachim de Flore utilisent contradictoirement. Dans le système johannique, figurent 900 ans (ou 1 000) comme « temps de royaume » du dieu et 1 260 ans comme phase de formulation avant le « royaume » et de « parvis ouvert », « d’exil » ou de dégénérescence après. Dans le système joachimique, 900 ans dénombrent le temps d’incubation du dieu et 1 260 ans le temps de sa formulation effective.

Dans la mesure où le nombre-clé e-1 peut s’écrire 12/7, il doit être partagé de même entre l’unité, qui ouvre la série des factorielles inverses, et les fractions qui suivent.

Si 1 + 1/2 + 1/6 + 1/24 + 1/120 + … = e-1 ou 12/7,

1/2 + 1/6 + 1/24 + 1/120 + … = e-2 ou 5/7.

En effet, e = 19/7, et 1 = 7/7, ainsi qu’on pouvait s’y attendre.

Le rapport entre l’unité et e-2 est encore 7/7 sur 5/7, c’est-à-dire 7/5…

Comme le démontre, même à ceux qui ne connaissent pas la constante e-1, la double étude de l’ésotérisme universel et de tout cycle correctement déterminé, où la dialectique temporelle, quelle qu’elle soit, épouse en effet le double rapport.

Cependant, il est clair que ce rapport même ne se vérifie qu’en certains cas particuliers ou, pour mieux dire, en un seul cas : au seuil absolu de la vie vécue ou de la durée accomplie; de même que le rapport de symétrie 6/6 ne se vérifie qu’en un moment de « l’amplitude de variation », où le sinus de l’angle inscrit égale 90 degrés et où le grand côté du triangle inscrit se confond avec la diagonale du carré.

Pas plus que je ne peux traiter de l’unité d’un cycle sans traiter de ses seuils successifs, de lecture ou de déliement, je ne peux nommer ces seuils sans définir les inversions de sens qui caractérisent le cycle, non seulement en son alternance propre (du jour, de la lunaison, de l’année, etc.) mais de la lecture de ses apparences au déliement de sa durée ou à l’inverse, puisque les moments de sa durée font aussi l’objet d’une « lecture ».

L’asymétrie – Si, en effet, je tente de figurer les seuils précédemment définis dans un schème qui pourrait les contenir tous, je me heurte dès l’abord à une contradiction apparemment insurmontable.

Tous les seuils se présentent comme doubles ou, pour mieux dire, dialectisés :

a) l’unité en q-1/q et q/q-1, selon que je la considère comme un objet de lecture ou un sujet (de délit). Mais la seconde est encore un objet de lecture, jusqu’à l’h barré, 12/9 ou tau-1, bien que ce ne soit plus une lecture « quantique », car la série : 12/11, 12/10, 12/9 n’offre pas la régularité de : 9/12, 10/12, 11/12 (au 1/12).

b) l’inversion cruciale autour de 1/2 et de 2. Mais cette croix non plus n’est pas symétrique. La couleur la plus « basse » se situe en 5/12 et non en 6/12. La note la plus haute en Si (1,81) et non en 12/7 (1,714) ou (e-1 : 1,718), achèvement de la « durée » : aucun de ces deux nombres n’atteint à 12/6.

Dans le croisement pseudo-symétrique, un chevauchement subsiste entre 6/12 et 5/12, une marge subsiste également entre 12/7 (La/Si) et 12/6.

c) le troisième seuil, le néant ou l’infini, n’est que numériquement symétrique : 0/q et q/0.

On le vérifiera par l’exemple par l’exemple qu’en donne la physique nucléaire, à l’approche du 0 absolu (-273° Kelvin).

Si le corpuscule observé est un fermion, c’est-à-dire une particule électronique polarisée de spin 1/2, il obéit au « principe d’exclusion » de Pauli, qui interdit à deux particules définies par les mêmes 4 facteurs de se situer sur la même orbite ou dans le même « espace de phase ».

Ces orbites étant définies par l’énergie du corpuscule, de son énergie maximale au point 0 (ou d’ionisation absolue), nous aurons, à l’approche du 0 absolu un certain nombre d’orbites porteuses d’une seule particule définie par les 4 facteurs.

Au contraire, si le corpuscule observé est un boson (soit un photon de lumière soit une particule d’hélium 4 ou l’atome neutre d’hydrogène), il n’obéit pas au principe d’exclusion. Toutes les particules, alors, tendront à se rassembler sur l’orbite 0 (ou la plus proche du 0 absolu), en même temps qu’à reformer la molécule.

Pour observer le phénomène – inobservable dans la « nature » – il faut donc interdire à la molécule de se reformer, en polarisant le boson, dans un champ magnétique intense. Mais, polarisée, la particule n’est plus un boson. Le recouvrement des parois du récipient expérimental par de l’hélium superfluide permettrait une observation de l’ordre de 9′, pendant lesquelles les particules se présentent comme des formativités sans masse et ne manifestent plus que des « effets quantiques », purement abstraits.

Pratiquement, au point 0 (à son approche), ou bien la particule témoigne d’une caractéristique nouvelle : l’ordonnancement exclusif, dans le cas du fermion, ou bien tend au rassemblement – dans l’incohérence ou le « révolutif », le retour à la forme antécédente.

Paradoxalement, c’est alors le fermion qui peut faire l’objet d’une lecture, puisque le principe d’exclusion le localise à l’approche de 0, quand le boson, en tant que tel, ne peut faire que l’objet d’une « manipulation ».

Nous retrouvons, à l’inverse, une inversion comparable à celle par laquelle j’ai défini l’Unité introuvable (entre 11/12 et 12/11) en situant la finalité AMOR dans le lisible, puisqu’elle seule à être « lue » (par l’observation du mouvement oculaire rapide).

Les deux inversions ne sont pourtant que comparables : elles ne peuvent être ni réellement inversées, ni même rattachées à un seul appareil : l’une, la dialectique SMOR/AMOR joue de minutes et même d’heures, la seconde, la dialectique fermion/boson, de millionièmes de seconde.

Mais il se peut qu’ici encore, le jeu mathématique permette ce que l’observation n’autorise pas.

Le jeu mathématique – Deux constantes nous ont permis de démontrer l’existence du seuil 12/11 et, donc, de son inverse : 11/12 :

h barré et tau-1, 1,054 et 1,154 de part et d’autre de 1,09,

1/h barré et 1/(tau-1), de part et d’autre de 0,91.

Puis la lecture de la longueur d’onde (liée à la vitesse de la lumière) nous a permis de localiser les couleurs dans le spectre : de 0,4 micron à 0,7 micron ou de 5/12 à 9/12;

l’étude de la quantité de mouvements, par celle de la fréquence (= e/h), nous a permis de mesurer les vibrations musicales, entre autres, de Ré à SI.

Le même nombre h barré a permis à Bohr de mesurer les charges énergétiques du fermion, sur chacune de ses orbites de déliement, depuis la plus proche de 1/2h barré² jusqu’au point 0.

L’énergie est inversement proportionnelle au rayon de l’orbite au carré. C’est-à-dire que :

On notera que 2h barré² = 1,1 X 2 = 2,2.

Ce nombre est très proche de la constante tau = 2,154.

Si bien qu’en me fondant sur tau-1 au lieu de h barré, je pourrai jouer de 1/tau au lieu de 1/2h barré².

Au contraire, les lectures temporelles de l’énergie d’un quantum de lumière (photon/boson) obéiront à la formule : E = HC/1.

C’est-à-dire que E sera inversement proportionnel à la longueur de l’onde.

On notera qu’ici encore, l’unité énergétique : 1 électron/volt ne se prend pas à l’unité de la longueur d’onde : 1 micron, mais à 1,24 micron.

Nous avons donc :

a) dans un cas

b) et dans l’autre

Ou, dans les deux cas, en jouant de tau, au degré de liberté près :

On notera que :

1) En valeurs absolues : C = 2,997 cm/s et h = 6,624.

C’est-à-dire que 1/tau = 0,464 équivaut (à 0,01 près : 0,474) à c/2π et à π/h.

C = 2π (1/tau)

h = π (1/tau)

hC = 2π2 ≠ 10 X 2 = 20 « à l’approximation près ».

2) Les nombres tau et 1/ tau offrent une particularité unique en mathématique :

Le nombre de Platon : 2 154 (pour 2 160) est tau à la puissance 10.

3) Cette stupéfiante équivalence : tau ³ = 10, tau⁶ = 100, tau⁹ = 1 000, etc. est à rapprocher,

d’une part, des tables de correspondance entre les longueurs d’onde et les fréquences des ondes électromagnétiques, où les longueurs jouent des 30 km aux 3 cm et les fréquences, dans l’ordre inverse, du kilohertz ou 10³ hertz au mégahertz ou 10⁶ et du méga au giga ou 10⁹.

10³ hertz = tau⁹ hertz

10⁶ h = tau¹⁸ h

10⁹h = tau ²⁷h

d’autre part, de l’estimation préhistorienne des grands cycles de l’humanité, puis de la vie animale, puis de la vie monocellulaire, puis de la matière elle-même, dans le même rythme :

30 X 10³ (l’homo sapiens), 30 X 10⁶ (30 X 10⁹), 30 x 10¹², etc.,

c’est-à-dire, encore : 30 X tau⁹, 30 X tau¹⁸, 30 X tau²⁷, 30 X tau³⁶.

Les 4 constantes – J’ai pu établir que (tau-1) est à l’h barré – à 0,1 près – ce que la constante (e-1) est à l’ancienne constante θ.

On remarque ainsi que :

(tau-1) + (θ-1) =(h barré -1) + (e-1) = √22/7 peu différente de √π.

Le parallélisme se maintient au-delà du nombre 2 :

θ + 1 = e moins 0,1 (2,618 pour 2,718),

ou en-deçà de 1/2 :

1/2h barré = 1/tau (0,45 pour 0,464).

Il y a donc bien correspondance entre les deux séries de constantes, comme le vérifie cette autre égalité, où apparaît de nouveau le nombre 10 (comme dans la série des puissances de tau) : 12 (θ + 1) =10π.

Et comme le vérifie le fait que les ésotéristes anciens, platoniciens ou hermétistes, taoïstes ou védiques, avaient pu formuler – imparfaitement ou non – la Machine de l’Etre sans connaître l’h barré ou (e-1).

Mais ils connaissaient 22/7 pour π; (1,256 + 0,9) pour tau; θ pour e-1 (ou, plus précisément, les hindouistes : 0,71 pour 0,718, 71 pour 71,8, etc.).

Il reste qu’un argument retient de considérer ces jeux avec sérieux : car, si les 4 constantes appartiennent en effet à des séries bien définies, aucune série connue ne les assemble toutes quatre par une seule fonction.

Moi-même, l’argument m’a retenu longtemps de voir en ces calculs plus que des coïncidences.

Mais la série existe, que fondait, voilà deux mille ans déjà, l’équation platonicienne, ou pythagoricienne selon la tradition :

(√5 +1)/2 = θ = √θ + 1

(θ = 1)/2 = √e-1.

Elle se laisse poursuivre dans un sens, avec un degré de liberté croissant puis nul, en :

(v12 + 1)/2 = √5 (2,236 pour 2,235)

(6 + 1)/2 = √12 (3,464 pour 3,5)

(11 + 1)/ 2 = 6

(21 = 1)/2 = 11

(41 = 1)/2 = 21

à l’infini.

Elle se laisse poursuivre dans l’autre sens, avec un degré de liberté croissant puis nul, en :

(√e-1 + 1)/2 = tau-1 = 1,154

et, pour x inférieur à √tau-1 :

(x + 1)/2 = √x

à l’infini.

La série des moyennes : (a + 1)/2 = b débouche sur deux infinis, l’un sans sommation finie, par une série divergente, pour a plus grand que 11, l’autre limitée à l’Unité : a = 1, par une série convergente, pour a plus petit que 1,077 ou √tau-1.

Nous y retrouvons les 3 phases :

a) convergente : (x + 1)/2 = √x

b) dialectique et appareillante pour les constantes :

tau-1, √e-1, θ, √5, √12,

c) ouverte à l’infini, pour les valeurs de a : 6, 11, 21, 41, 81, 161, 321, 641, 1281, etc.

Et notre trilogie : le Signe (unitaire), l’Appareil et le Seuil rend compte également de la triple étrangeté.

Les nombres fabuleux – On sait que h barré est le rayon d’un cercle de circonférence h (la constante de Planck). Ceci conduit à se demander si les constantes de la série des Moyennes ne pourraient pas être les rayons d’une série de circonférences non moins remarquables.

Si l’on a pu définir la constante h comme « les dimensions physiques d’une action » ou « le produit d’une énergie par un temps » ou « une énergie calculée par intervalle de fréquence », il apparaît que, sitôt quitté le cercle unitaire, où x = √x = 1, les moyennes déterminent de telles circonférences d’action ou de produits énergie X temps. Chacune d’elles est non seulement le rayon d’une telle circonférence mais son diamètre, moins l’Unité.

Par ses propriétés mathématiques et logistiques (chacune des moyennes ouvrant un « seuil de connaissance »), la série laisse loin derrière elle la série des nombres premiers.

Sa révélation au terme d’une si longue et si durable imprécision est comme un rire, une moquerie. Elle n’en est pas moins conséquente : si je ne peux déterminer ni l’Unité dans sa statique ni le Multiple en ses métamorphoses, ni l’origine de ma logique (le 1) ni son rapport même avec la réalité, quel autre recours me reste-t-il que l’établissement d’une moyenne – d’une infinité de moyennes – entre l’unité introuvable et la fuyante réalité?

N’est-il pas assuré, dès lors, que seule cette série de moyennes, depuis le néant jusqu’à l’unité et depuis l’unité jusqu’à l’infini, me permettra d’établir un rapport permanent entre Cela qui est et ce que je crois en savoir?

La plus grande rigueur, ici, ne contredit pas à la plus grande imprécision, mais elle en est l’aboutissement inévitable.

Jean-Charles Pichon