3
L’UNIVERS DES CYCLES
Autant nous avons vu les choses de l’espace – les formes géométriques entre autres – faire l’objet de calculs divers et de doctrines parfois contradictoires depuis 4000 avant J.-C., autant nous constatons que les choses du temps – les cycles temporels entre autres – ne font jamais l’objet que d’un unique calcul sur 6000 ans et plus.
Le zodiaque de Sumer était déjà un cercle, ainsi que nos pendules. Les 12 Signes annonçaient les 12 heures de l’horloge, les 12 mois de l’année, les 12 années du cycle d’activité solaire, les 12 ères précessionnelles de la Grande Année de Kepler, etc.
Plus surprenant : un rythme unique préside au double jeu du « jour » et de la « nuit » dans les 24 heures, de la croissance et de la décroissance des phases lunaires dans le mois, des saisons chaudes et des saisons froides dans l’année, des maxima et minima dans le cycle solaire, du réchauffement et du refroidissement de la terre entre deux ères glaciaires, mais également au double jeu de l’inspiration et de l’expiration de l’être vivant, des diastole et systole cardiaques, de la pousse de la végétation et de son déclin, de la constitution et de la corruption de tous les empires connus, etc.
Il n’est pas un cycle temporel que ne définisse une dialectique évidente : de la ténèbre et de la lumière, de la plénitude et de la disparition, de la croissance et de la décroissance, de la cohérence et de l’incohérence, de la vie et de la mort pour tout dire.
C’est pourquoi, divisés sans fin sur ce qu’il convient de croire ou de ne pas croire en ce qui concerne les apparences spatiales des choses : le bâton ou le serpent, le carré ou le cercle, l’onde ou le corpuscule, les esprits les plus opposés – le prêtre et le savant – ne disputent jamais du temps qui, de fait, les contient.
Mais cette unanimité ne va pas sans paradoxe. Car tous les hommes sont bien d’accord sur deux constatations contradictoires : le temps se laisse vivre comme une ligne droite et continue, du passé à l’avenir toujours; il ne se laisse étudier que sous la forme cyclique, comme une oscillation entre deux absolus : le tout et le rien, l’être et le néant.
Ce jour, lundi, n’est pas aussi longtemps que ses 24 heures n’ont pas été vécues; mais, sitôt qu’il est, il n’est plus : mardi a pris sa suite. Mon inspiration n’est accomplie qu’en ce point où je dois expirer. Quand le « royaume » d’un dieu survient : la Terre Promise ou le Temps de tous les Saints, le dieu atteint à son apogée et commence déjà de déchoir.
Le temps de dire : je ne respire plus, voilà que je respire de nouveau. Le temps de crier : Dieu est mort, voilà que, de nouveau, l’exigence mystique s’est emparée des hommes.
Cette continuité – la seule évidence – que tout le monde reconnait au temps, elle n’est faite, ainsi, que de discontinuités.
Mais cette dialectique encore s’exprime différemment à de différents niveaux.
a) En soi-même, comme Signe, le temps est à la fois une sommation quantique, dont le nombre q révèle le nombre de composants : 24 heures dans le cycle circadien mais 12 heures dans le cadran solaire ou dans l’horloge; 12 mois dans l’année ou 12 ères dans la Grande Année, mais 12 X 5 = 60 minutes dans l’heure, 60 secondes dans la minutes, – et une quantité aléatoire, à l’infini, de combinaisons éventuelles, cependant limitée par le nombre quantique qui me permet de nommer le cycle et sa partie : les jours de la semaine, le contenu de la semaine, les mois de l’année, les parties contenues dans l’année.
Dans sa totalité, le temps égale q X 1/q = 1;
dans sa partie vécue 1/q; dans sa partie restante 1 – 1/q; et dans le rapport – subjectif – entre la partie vécue et la partie à vivre :
(1/q)/(1 –(1/q)) = (θ-1)/(1- (θ-1)) = θ-1/2-θ = 0,618 = θ, si q égale le nombre d’Or.
(1/a)/(1 –(1/a)) = 1/(a-1) pour toute valeur de q.
b) En ce dernier rapport, le temps cesse d’être un Signe; il devient un appareil; il est doué d’un sens, tel que le Jour, l’Année ou l’Ere ne se fait pas sans se détruire, étant donné que la partie vécue (1/q) sera de plus en plus grande et la partie restante de plus en plus petite.
En ce sens, l’acquisition (de l’expérience) est une perte (d’innocence); l’association combinatoire se résout par une probabilité plus restreinte ou le développement du volume par un conflit croissant des particules massiques.
A la limite, l’accroissement de 1/q s’accompagne de la réduction de q (en l’Unité), jusqu’au point – inévitable – où q = 0.
A la dialectique : totalité/partie s’adjoint la dialectique tout autre : continuité/discontinuité, association/dissociation, que contiennent les deux dialectiques du Même (la même chose/la chose même) et de l’Autre (l’autre chose/la chose autrement).
c) Il s’ensuit que, dès lors, le temps se présente à la fois comme le contenant de la chose (sa propre existence) et son contenu, son moteur; ou bien comme le champ qui contient la chose, puisque le temps la déborde de tous côtés et comme le champ qu’elle contient; cyclique dans un cas, mais axé dans l’autre, de la naissance de la chose à sa mort par exemple.
Ce contenant et ce contenu jouent encore de la totalité et de la partie, du même et de l’autre, mais de telle sorte que je ne sais plus lequel est le tout et lequel la partie, lequel continu, lequel discontinu, du temps que mon existence limite et du temps qui me contient.
Car, hors du Signe et de l’Appareil, tout n’est ici question que de seuil.
Espace et temps – A première vue, cette trilogie temporelle recouvre donc celle que nous constatons en tout objet spatial, puisque elle se présente aussi comme le tout et la partie ou comme le même et l’autre ou comme le contenu et le contenant.
Elle en est cependant si distincte que, successivement, les chercheurs – tant scientifiques que religieux, tant réalistes que rationalistes – ont pu voir dans le Temps le Tout et dans l’étendue la partie, ou dans la chose du temps la chose même et dans les choses de l’espace des altérités, ou dans l’un le contenant, dans le second le contenu.
C’est qu’à la différence des formes de l’espace, je ne peux plus prétendre étudier les cycles, les formes temporelles, comme de simples figures, éventuellement conçues hors de toute matière ou de toute substance.
Si je peux me dépouiller des formes de l’espace (y compris de mon propre corps, comme Descartes), je ne puis m’arracher à ces formes du temps, car les cycles ne sont pas des « objets » de connaissance, au sujet desquels je puis m’interroger sur l’exactitude de ma connaissance : ils sont les outils mêmes de ma connaissance – et mon propre univers en soi.
Je vis de cette faim et de ce besoin de sommeil qui me prennent en effet tous les jours, des fruits et des légumes qui poussent en effet, à date fixe, tous les ans. Il n’est pas de pensée qui se libère tout à fait des émotions et des croyances liées à d’innombrables cycles : biorythmiques, lunaires, d’activité solaire, etc. Que je le veuille ou non, je ne suis pas le même la nuit et le jour, à l’aurore et au crépuscule, dans l’été ou dans l’hiver, sous la lune pleine et la nouvelle lune; mon grand-père ne pouvait être en 1888 ce que je suis en 1980. (1)
Si, donc, je puis parler de l’arc et de sa corde, du cercle et du carré, de l’onde et du corpuscule comme d’entités formelles et sans contenu réel, je ne puis parler des cycles comme de telles entités. Mais le jour demeure lié à la lumière du jour, le mois lunaire à la lune, l’an solaire au soleil, à la pousse de l’herbe et de toute végétation; des cycles plus vastes, de 180 ans ou de 2 000 ans, demeurent liés aux marches des planètes, à leurs aspects, leurs conjonctions; plus petits, de quelques heures ou de quelques microns, aux vibrations de mes fosses nasales ou aux vibrations du césium.
Il n’est pas de temps qui ne soit l’existence même d’un corps, d’un animal, d’un végétal ou d’une planète, d’une particule ou d’une cité.
Son étude, par suite, ne peut pas être abstraite. Elle ne peut procéder que d’une constatation. D’où, enfin, l’impuissance où je suis de traiter du problème des cycles comme d’une généralité. Je ne peux traiter que de ce cycle-ci ou de celui-là. Soit, précisément, de ces quatre dont j’ai choisi de parler : le mois lunaire, l’année solaire, le cycle des activités solaires, les cycles d’aspects et de conjonction des planètes les plus éloignées, parmi des centaines d’autres sujets possibles.
——————————————————————————————–
(1) Par exemple, les organismes vivants contiennent moins de calcium à 11 heures le matin ou le flux électromagnétique dans l’atmosphère terrestre est plus puissant deux heures après le coucher du soleil et deux heures avant son lever, au point où ces lever et coucher se constatent.
Le mois lunaire – Le mois lunaire devrait être la durée précise du voyage de la lune autour de la terre, c’est-à-dire 27 jours et 8 heures. Mais on entend par « mois lunaire », généralement, l’intervalle entre deux pleines lunes ou deux conjonctions lune-soleil : 29 jours 499/940 en moyenne, qu’il vaudrait mieux nommer une « lunaison ».
Le décalage entre le mois lunaire et la lunaison s’explique par le mouvement précessionnel du Soleil (ou du 3ème mouvement de la Terre, selon Kepler) qui « décale » l’astre de quelque 30 jours par an ou 2,5 jours par « mois ». En sorte que la lune, en son voyage, ne rejoint le soleil que 2,5 jours (plus ou moins) après tour de 27,33 jours. Mais d’autres explications, avant Hipparque, et de nouveau entre Ptolémée et Kepler, avaient été données au phénomène; d’autres en seront données demain.
L’ésotérisme calendérique suppose au mois lunaire/lunaison la durée moyenne de 28 jours ou de 4 semaines de 7 jours. Pas plus que les 28 jours ne contiennent une lunaison réelle, les 7 jours ne contiennent un quartier de lune.
La simple lecture du calendrier révèle que les quartiers (nouvelle lune, premier quartier, pleine lune, dernier quartier) ont une durée – très imprécise – de 7 à 9 jours en moyenne, avec une durée excentrique de 6 jours seulement tous les 3 mois environ. En tenant compte de cette excentricité, la moyenne du quartier est de 7,5 jours ou 30/4.
Une durée toute différente, calendérique et non réelle, prête au mois la « valeur » d’1/12 d’année solaire ou 365,25/12, peu différente de 30,5 jours.
Mais, ici encore, les calendriers offrent des différences relativement importantes. Le Tchong-ti chinois compte 30 jours 7/16, avec une exactitude très remarquable. Les mois antiques (sumériens, babyloniens) ne recouvraient que 30 jours ou le 1/12 de 360.
Une conséquence de ces différences est que le rapport mois/douzième de l’année ou lunaison/ »mois » solaire joue des 28/30 ou 14/15 dans l’ésotérisme traditionnel, mais de 228/235 dans le décompte chinois ou coranique, puisque le Coran également se fonde sur l’équivalence des 19 années solaires (228 « mois » solaires) et 235 lunaisons (ou 19 « ans » lunaires et 7 mois).
Nous disposons donc d’une grande variété de mois : 27,33 jours, 28 jours, 29,5jours, 30 jours, auxquels s’ajoutent nos mois occidentaux et, plus spécialement grégoriens : 28, 29, 30 et 31 jours.
Si je définis le mois comme une lunaison, le choix, plus restreint, s’inscrira entre 29,5 et 29,9 environ; mais il sera encore beaucoup trop considérable pour prétendre à une précision parfaite. D’autant plus que les 4 phases lunaires ne s’offriront pratiquement jamais au 1/4 de la lunaison.
De l’invraisemblable degré de liberté mensuel : 3,66 jours entre 27,33 et 31, nous serons passés à un degré de liberté non moins considérable de 3 jours entre 6 et 9. Mais, alors que le premier joue de 1,88 autour de 29,5, au 1/15, le second joue de 1,5 autour de 7,5, au 1/5. Il est donc trois fois plus grand.
L’année solaire – L’Histoire témoigne que tout rationalisme privilégie un cycle temporel aux dépens des autres : ce put être le « jour » dans le Moyen Empire égyptien ou le « mois lunaire » dans l’Inde hellénistique. C’est assurément « l’an solaire » depuis le concile de Trente et l’avènement du rationalisme contemporain.
Il suit que l’année de 365,25 jours 9′ 9″ nous est donnée comme d’une précision rigoureuse, quasi miraculeuse en regard de l’imprécision qui règne partout ailleurs.
Or, il est possible que l’estimation du pape Grégoire ait correspondu très exactement au cycle annuel ainsi qu’il pouvait apparaître aux observateurs en la fin de notre 16ème siècle.
Il se peut même que des observations analogues aient été faites en de certains moments de l’Histoire égyptienne, tels que vers -2800, ou 1 460 ans plus tôt, ou 1 460 ans plus tard, puisqu’il semble bien que 1 460 ans (= 4 X 365) ait été une « ère » égyptienne sur plus de 4 000 ans : 4 380 ans (= 3 X 1 460) de -4260 au règne de Trajan, où Tacite souligne encore la persistance de la croyance.
Mais nous savons d’autre part que des durées différentes ont été données à ce cycle en des époques différentes et par des hommes dont la culture valait bien celle des Anciens Egyptiens. Platon tient pour les 360 ans, Mahomet pour un cycle de 361 ans (19 X 19), l’Ecole d’Alexandrie pour 365 ans; les 13 mois lunaires (de 27,33 jours) ont eu des défenseurs jusqu’en Extrême-Orient : 13 x 27, 33 = 355,30.
Nous savons également que, depuis la fondation de l’antique Babylone, au 19ème siècle avant J.-C., les rois et les pontifes n’ont presque pas cessé de modifier le calendrier existant, soit pour y ajouter un mois tous les siècles, soit pour en retrancher quelque décade.
Au temps de Jules César, l’année dépasse les 400 jours et Jules César lui-même fait « allonger » l’année. A la fin du 16ème siècle, Grégoire fait supprimer 10 jours pour retrouver le cours réel du temps.
Si l’on tient compte des modifications, dont nous ne savons le détail, qui eurent lieu en Grèce lors de la fondation des Jeux (au 8ème siècle avant J.-C.), dans les pays hellénistiques après la mort d’Alexandre (en -312),lors de la constitution de l’Islam, après la mort de Mahomet, et, vers la même date, en Occident, lors de la constitution du calendrier chrétien, etc., il nous admettre que, tous les cinq siècles plus ou moins, le cycle solaire est remis en cause.
Nous nous ne pouvons en déduire qu’au cours des 15 siècles égyptiens ou des 21 siècles précessionnels, le cycle solaire subit les mêmes modifications que le cycle lunaire en 180 ans plus ou moins. Mais il semble assuré du moins que les variations saisonnières dans l’année solaire sont du même ordre que les variations des quartiers lunaires dans la lunaison. Si le degré de liberté joue ici de 3 jours par quartier ou de 1,5 jour autour de 7,5 jours, il peut jouer, là, de quelque 10 ou même 13 jours autour de l’équinoxe (comme du 2 au 23 septembre ou comme du 20 mars au 16 avril). (1) Ce qui n’empêche pas de donner à la « saison » une durée moyenne de 3 mois et de 90 jours.
———————————————————————————————
(1)Voir, au chapitre suivant, l’expérience du Massachusetts.
Le cycle d’activité solaire – A première vue, ce cycle est tout autre que les précédents.
En effet ces derniers se présentent comme des cycles de relation (lune/terre) et de conjonction (lune/soleil) ou de révolution (de la lune autour de la planète Terre, de la Terre autour du Soleil). Au contraire, le cycle d’activité solaire est un cycle « modal », lié à la vie de l’astre en soi.
Cependant, les quartiers de la lunaison révèlent que le cycle de conjonction s’accompagne d’un cycle d’aspects (nouvelle lune, pleine lune, etc.) et les saisons révèlent que le cycle de révolution terrestre s’accompagne d’un cycle modal, de réchauffement et de refroidissement de la Terre en soi.
L’hypothèse est donc rationnelle que le cycle modal d’activité solaire s’accompagne d’un cycle relationnel encore ignoré. Si les mêmes causes produisent les mêmes effets… puisque le double rythme : maximum/minimum et à l’inverse semble analogue aux rythmes des aspects lunaires : pleine lune/nouvelle lune et à l’inverse, et aux rythmes saisonniers : d’un solstice à l’autre.
De fait, un cycle de révolution, celui de Jupiter, apparaît analogue au cycle d’activité solaire (l’un de 11,7 ans, l’autre de 11 ou 12 ans en moyenne) et la confusion devait donc s’opérer entre les deux cycles, comme entre le cycle de révolution de la lune et la lunaison ou entre le cycle de révolution de la terre autour du soleil, d’une part, et les saisons terrestres de l’autre.
Mais l’hypothèse se heurte à la même contradiction que les deux hypothèses précédentes : comme la révolution lunaire et la révolution terrestre, la révolution de Jupiter apparaît relativement régulière (quelque 11,7 ans, peu différents de 12). Comme les quartiers lunaires et les saisons terrestres, les minima et maxima solaires se révèlent des plus irréguliers.
Depuis que le cycle fait l’objet d’une observation systématique (depuis 1871), l’alternance obéit aux nombres :
d’un maximum à l’autre : minimum en :
1871/1885 (14 ans) 1878
1885/1894 (9 ans) 1889
1894/1905 (11ans) 1901
1905/1917 (12 ans) 1912
1917/1928 (11 ans) 1923
1928/1937 (9 ans) 1933
1937/1947 (10 ans) 1943
1947/1957 (10 ans) 1953
1957/1968 (11 ans) 1964
1968/1980 ? 1976
Au moment où j’écris – décembre 1980 – je ne saurais dire si le maximum a été atteint cette année ou s’il ne sera pas dépassé l’an prochain, car tous les 9 cycles environ, le degré de liberté du cycle, relativement réduit en règle générale (de 9 à 12 ans) connaît un brusque débordement, jusqu’à 14 ou même 16 ans, comme du maximum de 1788 à celui de 1804.
Ce n’est pas dire que le cycle a.s. (d’activité solaire) est plus irrégulier que les précédents. S’il comporte son « excentricité », tous les dix cycles environ, comme, d’ailleurs, les cycles lunaire et solaire, on voit que, pour le reste, son degré de liberté ne déborde guère les 3 ans (de 9 à 12) et, plus précisément, 1,5 an autour de 11,1 ans.
Puis, de même que le « mois » joue entre les 27,33 jours du cycle lunaire et les 31 jours de certains mois, et « l’année » entre les 13 mois lunaires de 27,33 jours et les 12 mois solaires de 28 à 31 jours, nous voyons que le cycle a.s. joue entre les 12 années ésotériques de 360 jours (4 320 jours), le cycle jupitérien de 4 273,425 jours (11,7 X 365,25) et le cycle « modal » de 4 054,275 jours en moyenne (11,1 X 365,25).
L’écart maximum entre ces trois cycles : 4 320 – 4 054, est de 266 jours, pour un degré de liberté de 133 jours autour de 4 187 jours, nettement inférieur au degré de liberté du cycle lunaire.
Mais, à première vue, si je prétends partager le cycle a.s. en quatre parties égales, à l’image du quartier lunaire ou de la saison terrestre, le calcul en sera beaucoup plus incertain.
Il est possible, cependant, que cette incertitude tienne, entre autres causes, à la confusion qui s’opère actuellement entre, d’une part, la croissance et la décroissance des « taches » (ultraviolettes) à la surface de l’astre et, d’autre part, la croissance et la décroissance de l’activité solaire proprement dite.
En effet, pour que ce parallélisme puisse être soutenu, il faudrait évidemment que l’absence totale de taches correspondît à un minimum de l’activité.
En effet, pour que ce parallélisme puisse être soutenu, il faudrait évidemment que l’absence totale de taches correspondît à un minimum de l’activité.
Il n’en est pas ainsi : la première apparition des taches précède de plusieurs mois le minimum a.s. Soit, dans les deux derniers cycles :
Maximum les taches Minimum
décembre 1957 août 1963 septembre 1964
août 1968 janvier 1975 mai 1976
—————- —————– ———————-
10 ans et 8 mois 11 ans et 5 mois 11 ans et 8 mois
quart : 32 mois quart : 34,75 mois quart : 35 mois
Sur cet exemple, on pourrait prétendre que le « quart » du cycle a.s. joue de quelque 36 mois ou 3 ans, c’est-à-dire 12 saisons solaires et 144 quartiers de lunaison. Mais l’examen des cycles depuis 1871 réduit cette moyenne à 2,8 ans ou 33 mois.
Il reste que, autour de cette moyenne, le degré de liberté des « quarts » jouerait de quelque 9 mois (de 24 à 42) autour des 33 : il serait donc analogue aux degrés de liberté notables dans le quartier lunaire : 1,5 jour autour de 7,5 jours, et dans la saison terrestre : quelque 9 jours autour de 81 jours.
Quoique plus important :
9/33 = 3/11 = contre 1/5 (le degré de liberté du quartier) et 1:9 (le degré de liberté de la saison).
Une remarque – Sans en tirer aucune conclusion pour l’instant, je ferai au sujet de ce quart du cycle (quartier, saison) et de son degré de liberté la double remarque suivante :
1) le degré de liberté ne devient irrégulier que si je tiens compte, dans son calcul, du « quart excentrique » : un quartier lunaire de 6 jours, une saison de 72 jours, un « quart » du cycle a.s. de 3,75 ans.
Mais, en dépit de cette irrégularité, la moyenne du quartier ou de la saison apparaît comme parfaitement stable :
le quartier lunaire à 7,5 jours ou 180 heures (ou, sinon, aux 11/12 de 180 : 165 heures),
la saison terrestre à 90 jours (ou, sinon, aux 11/12 de 90 : 81 jours),
le quart de l’activité solaire à 3 ans (ou, sinon, aux 11/12 de 1 080 jours (3 X 360), c’est-à-dire 972 jours).
Le quartier lunaire est donc au 1/12 de la saison terrestre et celle-ci au 1/12 du « quart » solaire.
2) Si je ne tiens pas compte du « quart excentrique », le degré de liberté de ces divers cycles recouvre une parfaite régularité : au 1/6 du quart ou au 1/24 du cycle :
de 1,25 jour en 30 jours (comme de 7 à 8,25 jours),
de 15 jours en 360 jours (comme de 77 à 92),
de 6 mois en 12 ans (comme de 2,2 à 2,8 ans).
Ce sont alors les degrés de liberté eux-mêmes qui s’inscrivent l’un en l’autre :
le degré de liberté dans la lunaison au 1/12 du degré de liberté dans l’année solaire et celui-ci au 1/12 du degré de liberté dans le cycle d’activité solaire.
Du plus grand au plus petit :
chacun des « quarts » théoriques (sans tenir compte du quart excentrique) comporte un degré de liberté au 1/12 du précédent,
chacun des « quarts » effectifs ou réels (y compris le quart excentrique) se présente, en moyenne constante, comme au 1/12 du précédent.
Les cycles d’aspect planétaire
Malgré leurs degrés de liberté, sinon l’incertitude qui demeure en leurs calculs, la réalité des cycles précédents n’est mise en doute par personne.
On discutera de leurs causes, apparentes ou non, comme il semble que le soleil tourne autour de la terre mais qu’on s’assure du contraire et que c’est la terre qui tourne. Ou comme certains rapportent le cycle lunaire à la marche de notre satellite dans l’espace et d’autres esprits aux conjonctions soleil-lune. Ou comme le cycle a.s. apparaîtra lié tantôt à la vie de l’astre (à des déplacements rythmiques de matière depuis son centre vers la surface), tantôt à d’autres conjonctions entre le soleil et les planètes. Etc.
On discutera aussi, bien sûr, de leurs influences. Celle du cycle annuel sur les saisons terrestres est aujourd’hui la seule admise par tous (il n’en fut pas toujours ainsi). Mais l’influence la plus remarquable, la plus sensible à l’être humain et que la majeure partie des peuples, sur des dizaines de siècles, a pu considérer comme la plus assurée : l’influence du cycle lunaire, est aujourd’hui niée par nos éducateurs. Quant au cycle a.s., d’invention récente, il est bien naturel que nous ne sachions qu’en penser.
Mais ces discussions ne concernent pas l’existence des cycles. Il n’en va pas de même en ce qui concerne les cycles plus étendus, qu’on nommera de conjonctions ou d’aspects planétaires (a.p.). Cela est d’autant plus surprenant que ces grands cycles, d’autre part, appartiennent à l’héritage le plus constant et le plus ancien de la culture humaine.
Le cycle de 180 ans fut connu des Alexandrins; celui des 360 ans (ou 361, ou 366) de Mahomet et de Platon; celui des 2 000 ans plus ou moins des brahmanes indiens, des prêtres égyptiens et des auteurs du Livre d’Enlil, deux millénaires avant le Christ, etc. Mais, plutôt qu’aux marches de planètes, dont on nous dit du reste qu’elles étaient ignorées il y a seulement deux siècles (Neptune, Uranus, Pluton), on attribuait ces cycles aux signes zodiacaux, aux anges ou aux démons. Ils étaient connus mais attribués à des « causes » tout autres que celles que nous leur connaissons. Constatés – au plan de l’ésotérisme – ils n’étaient pas connus – au plan rationnel.
C’est ce qu’on nous dit, du moins, et ce qu’on croit… jusqu’au jour où l’on retrouve les notes de Galilée relatives à l’emplacement de Neptune, ou la mention des « 12 planètes » en de certains ouvrages hermétiques, ou la cotation précise de planètes inconnues de nous (le Dragon, Dumuzi, la planète x) dans la Chine antique ou l’antique Lagash mésopotamienne.
Je crois que, de tout temps, un esprit rationnel a préféré pouvoir rapporter aux planètes – visibles – plutôt qu’à des Signes – invisibles – la permanence des cycles qu’il devait constater sans en déceler la cause.
Je donne peu de références en cet essai, car le moment vient où la mémoire ne sait plus – et ne doit plus savoir – d’où elle tire ses trésors. Mais je suis contraint, ici, de citer l’ouvrage, récent et encore inconnu, de Pierre Cormier : Après le temps des prophètes (Acturus 1980).
Je ne donne pas ce livre comme comparable aux grandes sources de la connaissance : livres sacrés, philosophies systématiques, créations mathématiques, etc. Le souci d’une causalité arrête l’auteur au seuil des illuminations; sa méthode est très astucieuse, mais malheureusement il la prend au sérieux; son rejet de l’ésotérisme traditionnel en Occident (de l’ère précessionnelle, entre autres) et son admiration inconditionnée de l’ésotérisme chinois (le Yi King) ne se fondent sur d’autres bases que sa propre croyance, etc.
Mais le livre est honnête, et c’est assez pour le distinguer parmi tous les écrits, plus ou moins délirants, qui pullulent en notre époque. Une preuve absolue de cette honnêteté est assurément que, rejetant la croyance aux ères précessionnelles, l’auteur en démontre la réalité, sans seulement en prendre conscience. Une autre preuve en est que ses nombres, évidemment, ne sont en rien systématiques : il les donne pour ce qu’ils sont, et ne parvient pas sans peine, ensuite, à les interpréter dans le sens qu’il voudrait leur donner (un sens doublement inspiré par l’ésotérisme chinois et les théories de Spengler).
Mais ses nombres demeurent, non différents de ceux qu’on trouve ici et là, pour une fois rassemblés. on doit souscrire aussi, je crois, à son partage trinitaire entre les planètes « lentes » ou « éloignées », les planètes moyennes et les planètes « rapides » ou proches du soleil, partagé fondé somme toute sur les « niveaux » de révolution : de 80 ans à deux siècles et demi, quelques dizaines d’années, plus ou moins l’année terrestre; et à son partage, par suite, des aspects planétaires en trois niveaux clairement définis.
Je m’en tiendrai, pour cette étude, aux deux premiers niveaux, que P. Cormier partage en trois trigrammes d’aspects et de conjonctions :
a) plutoniens : Neptune/Pluton,
Uranus/Neptune,
Uranus/Pluton.
b) saturniens : Saturne/Uranus,
Saturne/Neptune,
Saturne/Pluton.
c) jupitériens : Jupiter/Saturne,
Jupiter/Uranus,
Jupiter/Neptune.
Et, pour le reste, ne retiendrai, de l’étude de P. Cormier, que les partages des aspects en 8 degrés de conjonctions, depuis le 0 (pas de conjonction) jusqu’au 7 (le ciel le plus peuplé), puisqu’il suffit pour établir, dans la marche complexe des planètes, les « positionnements » les plus remarquables, ainsi que les phases d’ordre ou de désordre apparentes dans la succession des 8.
Les figures d’une danse – Les travaux de l’auteur font apparaître :
– d’une part, que, dans chaque ensemble de trigrammes, les séries d’aspects suggèrent une danse des planètes, où tantôt les corps célestes s’éloignent les uns des autres, tantôt se rapprochent au plus près. Assez justement, P. Cormier compare ces mouvements contraires à la dialectique cardiaque : systole/diastole;
– d’autre part, que ce mouvements, tantôt n’offrent aucune régularité, tantôt présentent une régularité parfaite, qui se répète en effet au bout de certaines périodes et s’offrent ainsi comme les figures d’un ballet.
Parmi les tables qu’il en donne, la plus significative peut-être, en ce qu’elle confirme l’existence du cycle de deux millénaires (que, par ailleurs, l’auteur méprise), porte sur les séries de trigrammes plutoniens.
Elle établit, sur des périodes de quelque cinq siècles, l’alternance de séries régulières puis irrégulières, selon le schème :
5, 1, 5, 7, 3, 1 de 5 à 7 ou de 0 à 2
(régulier) (plus ou moins régulier)
-3105/-2934 -2881/-2613
-2613/-2419 -2374/-2130
-2076/-1905 -1874/-1615
-1563/-1392 -1380/-1137
De -1137 à +806, le jeu se renouvelle, sur 4 nouvelles phases de quelque 500 ans, mais l’ordre de régularité est alors : 1, 3, 7, 3, 1, 5, 7.
Le jeu se renouvelle à partir de 837 et semble devoir être mené jusqu’en 2773, avec un ordre de succession régulière très comparable à celui de la période : -3105/ -1137.
Si bien que nous avons, sur quelque six mille ans :
– trois grands cycles répétitifs, de quelque 1 950/1 980 ans l’un,
– en chacun de ces cycles, quatre phases de quelque cinq siècles l’une, dont le rythme d’alternance rappelle évidemment les rythmes dialectiques : croissance/décroissance, refroidissement/réchauffement, accroissement/réduction d’activité, des cycles plus connus.
Quant aux deux cycles de 1 980 et de 490 ans (plus ou moins), ils se présentent exactement comme des correspondances planétaires aux grands cycles ésotériques de 2 160 ans et de 540 ans, au 1/12 près.
Des ballets analogues, mais sur des durées moindres, peuvent être évoqués à partir des calculs relatifs aux trigrammes neptuniens, saturniens, jupitériens, etc. En sorte que le champ planétaire tout entier n’apparaît plus à l’astronome que comme une immense salle de danse.
Des saisons séculaires – En étudiant de plus près les divers cycles, on constate avec étonnement – ce que Pierre Cormier n’a pas clairement su voir – que :
1) la période que nous vivons présente une succession d’aspects plutoniens rigoureusement identique à celle de la période -2076/-1905, sur 4 000 an, et similaire, par sa régularité, à celle de la période -148/+64, sur quelque 2 000 ans.
Exactement :
de -2076 à -148 : 1 928 ans et de -148 à 1868 : 2 016 ans
de -1905 à +64 : 1 969 ans et de 64 à 2039 : 1 975 ans
sur 2 016 + 1 928 = 1 975 + 1 969 = 3 944 ans, alors que les « ères » ésotériques donneraient : 2 160 + 3 160 = 4 320 ans;
2) dans l’ère actuelle (depuis 837), la même période présente de précises concordances d’aspects (5, 1, 5, 7, 3, 1) de 1863 à 2047, avec les périodes :
937/1031, sur 194 ans,
1354/1539, sur 185 ans,
avec des écarts de : 517 ans (837/1354) et 509 (1354/1863),
et de : 509 ans (1031/1539) et 508 (1539/2047).
Notamment, l’identité plutonienne est presque parfaite entre :
918/983, 1445/1499, 1909/1918 (6, 2, 0, 1, 5, 7, 6, 2, 0, 4…7, 3, 1, saturniens).
3) dans les cycles d’aspects moindres (saturniens/jupitériens) les successions d’aspects se renouvellent – moins exactement dans l’ordre, mais rigoureusement quant aux durées des phases – entre :
1592/1624 et 1963/1993, avec un écart de 371/369 ans et 1360/1642, 1800/1821, 1980/2000, avec un écart de 180 ans.
Esotériquement, nous retrouvons ici les grands nombres classiques : 180 ans – 360 ans (à 10 ans près) – 540 (508/519) et 2 160 ans (1928/2016), ce qui nous autorise à y appliquer les grandes divisions zodiacales et la concordance classique entre l’ère de 2 160 ans et l’année, la phase de 540 ans et la saison, la phase de 180 ans et le mois.
En 1868/2039, nous sommes dans la même « saison » du Verseau qu’en -2076/-1905 dans le Bélier et en -148/+64 dans les Poissons : l’éveil du mythe nouveau au début de l’été;
dans la même période de crise qu’en 837/1050 et 1354/1539, 1ère saison (l’hiver) et 2ème saison (le printemps) de « l’année » précessionnelle;
dans une période équivalente à celle de 1592/1624, depuis 1963 et jusqu’en 1995, dans les 360 ans. cette période est essentiellement messianique : 1592/1624 fut celle des Rose-Croix, des Sikhs, des derniers grands prophètes de l’Islam, etc.;
dans une période rythmiquement équivalente à celles de 1620/1642 et 1800/1821, depuis l’année 1980 jusqu’en 2000, dans les 180 ans ou au 1/12 de l’ère.
1620 a marqué le renouveau des Gémeaux (conformité, mode, fraternité, l’observation scientifique), proclamé trente ans plus tard, par les sectes nouvelles, les Carmes, Louis XIV et ses courtisans, les Académies et les sciences, de Digby à Newton.
1800 a marqué le renouveau du Cancer en ses deux figures éternelles : l’Empire et le Savoir.
1980 devrait marquer le réveil du mythe de Hiérarchie (le Lion).
Nous sommes donc, astrologiquement, à l’apogée d’une ère précessionnelle, au début de son été et au début d’un « mois » précessionnel de 180 ans.
Mais, surtout, nous ne pouvons douter que les cycles d’aspects planétaires ne sont pas plus indépendants les uns des autres que le mois de la saison et celle-ci de l’année.
Comme l’année elle-même s’inclut dans le cycle, douze fois supérieur, de l’activité solaire, il nous devient possible d’imaginer que l’ère de 2 160 ans s’inclut dans un cycle douze fois supérieur : la Grande Année de 25 920 ans, au degré de liberté près.
C’est-à-dire d’établir la double série de cycles :
le mois la saison l’année le cycle a.s.
180 ans 540 ans 2 160 ans 25 920 ans
1 3 12 144
L’obstacle réside ici dans la très grande incertitude qui touche à la saison (le quartier, le quart du cycle) et dans la relative approximation du cycle lui-même.
Cette approximation n’est pas considérable. Elle joue du 1/12 plus ou moins : 180 ans sur 2 160, 1 an sur les 12 ans du cycle a.s., 1 mois lunaire dans l’année solaire, etc.
Mais le degré de liberté relatif à la saison apparaît plus considérable :
le quartier lunaire joue de 6 à 9 jours,
la saison de 2,5 mois à plus de 3 mois,
le quart du cycle a.s. de 2,2 ans à 3,6 ans,
les 540 ans du cycle plutonien des 492 ans Neptune/Pluton à une durée inconnue, puisque nos calculs ne portent que sur 6 000 ans.
L’indétermination ne pourrait que s’accroître si nous traitions de cycles plus vastes, comme de la « saison » de 6 480 ans dans la Grande Année de 25 920 ans.
Nous voyons qu’en effet, elle semble tenir au double caractère : contenu/contenant du cycle considéré.
C’est ainsi que l’orbite lunaire est considérée tantôt comme contenante de la terre, autour de laquelle la lune tourne (en 27,33 jours), tantôt comme contenue dans le système solaire, que la lune parcourt en 29,5 jours, d’une conjonction solaire à l’autre.
L’orbite terrestre est considérée tantôt comme contenante du soleil, autour duquel la terre tourne (en 365,25 jours), tantôt comme contenue dans le système solaire et la majorité des aspects planétaires, tels que les aspects jupitériens, saturniens et plutoniens.
Le soleil lui-même, « contenant » de la terre, puisqu’il l’inonde ou non de ses radiations, est contenu dans son système, puisque toutes les planètes y entrent en conjonction avec lui. D’où par exemple, les deux cycles d’activité solaire (11,1 en moyenne) et de conjonction jupitérienne (11,7 ans).
Il est donc assuré que les cycles d’aspects, de même, doivent offrir une double lecture. Mais, de ces deux lectures, une seule nous est permise : celle du cycle contenant, puisque nous ne savons « en quoi » les cycles d’aspects se meuvent et ne connaissons même pas l’exacte dimension du système solaire, si, comme il est probable, d’autres planètes existent au-delà de Pluton.
Les autres cycles – On me reprochera sans doute de borner mon étude aux quatre cycles lunaire, annuel, solaire et planétaire (fragmentairement). Je n’ignore pas l’engouement contemporain pour les biorythmes et je ne peux négliger les innombrables cycles inventés ou réinventés depuis un demi-siècle : biologiques et nucléaires entre autres.
Mais :
a) ou bien des cycles se présentent comme des lectures différentes des cycles définis. Par exemple, les biorythmes demeurent clairement liés au cycle de la lunaison : non seulement leur rythme s’y compare, mais leurs maximum et minimum y correspondent (dans les 23, 27 ou 33 jours), comme Charles Barzin l’établit (« La représentation des Cycles », Co-incidences n°9, I.N.A.C. 4020 Liège).
b) ou bien ces cycles se présentent comme individuels : le cycle de la respiration ou celui du rêve ne sont pas rigoureusement identiques chez tel ou tel individu. Celui du carbone 14 n’est pas celui du radium b, etc.
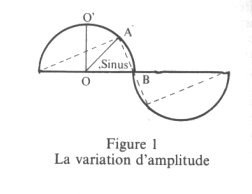
Mais l’onde modèle s’y reconnait toujours, les différences entre les courbes possibles ne tenant qu’à la variation de leur amplitude, c’est-à-dire au choix du point d’origine A sur la circonférence théorique et à sa projection sur l’axe vertical 00′, c’est-à-dire au sinus de l’angle AOB (figure 1).
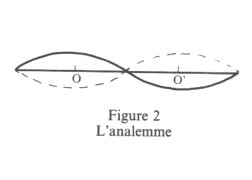
Or, l’objet de cette étude est précisément de déterminer si, en dépit de la variation d’amplitude – et de la liberté individuelle, qui en découle – quelque modèle cyclique d’univers peut ou non recouvrir tous les cycles temporels, réels ou éventuels, quelle que soit leur nature. C’est-à-dire de rendre compte de toutes les variations imaginables, dans l’hypothèse non seulement que formule la figure 1 mais que peut formuler une double ellipse quelconque (l’analemme de la figure 2) : l’ondulation multiforme du serpent-réalité.
Jean-Charles Pichon 1980