LA MACHINE DE L’ETERNITE

Pour Elisabeth à qui l’écriture de ce livre doit tant et sa publication doit tout.
J.C.P.

Préface

Cette étude se présente comme la conclusion d’une quête de vingt-trois ans initialement historique : la reconnaissance et le recensement des croyances humaines de tous les temps et de tous les pays. Les ouvrages que j’ai publiés entre 1958 et 1973 rendent compte de la recherche et de ses résultats : la mise en lumière de cycles peu connus il y a vingt ans et encore méprisés ou méconnus de nos jours : le cycle d’activité solaire, une phase de quelque 180 ans, l’ère précessionnelle de 2 160 ans, etc. Mais, bornés par leur objet même, ces ouvrages n’offrent aucune étude du cycle en soi, non plus qu’aucune explication satisfaisante pour un esprit contemporain des « éternels retours » cycliques. J’y constate les retours, en forme de syncrétismes, des principales croyances humaines et des mythes majeurs qui les fondent, mais je n’en décris pas le mécanisme, lié à ce qu’on doit nommer la mécanique de l’Etre, car une telle mécanique m’était inconcevable il y a dix ans.
Au contraire, je répétais fréquemment, alors, que la constatation mythologique, de même que l’observation scientifique, ne procède pas – et ne doit pas procéder – d’un a priori logistique (mathématique, métaphysique ou simplement déductif). Cela est ainsi, voilà tout.
Mais, les dernières lignes écrites qui achevaient L’histoire des mythes et La vie des dieux, une autre exigence m’a saisi : la résolution d’un problème dont j’avais posé les données. Ou, plutôt : non pas sa résolution, car je ne pouvais prétendre à réussir, là où le génie humain n’a pas cessé d’échouer. Mais son analyse méthodique et peut-être, même, exhaustive, si le temps m’en était laissé.
Dès lors, abandonnant le recensement historique des mythes et des croyances, j’ai entrepris une tâche toute différente, où le recueillement primait la lecture, le calcul la constatation, le raisonnement l’accueil. Si différente que, me semble-t-il, d’autres liens ne rattachent cette quête-ci à la précédente que la rigueur la plus épurée et la passion du jeu la plus gratuite apparemment.
Car, ici comme là, j’ai dû m’attacher à joindre les contraires les moins conciliables : naguère, le respect de doctrines très diverses et leur incessante remise en question; hier et aujourd’hui, l’application systématique de principes et de formules mathématiques qu’il m’est interdit de tenir pour éternels ou absolus mais dont il me faut jouer comme de sûres approches de l’éternel ou de l’absolu. Toutes les dialectiques contenues dans le mot que j’avais trouvé en 1957 : le réalisme irrationnel mais que je devais, pour poursuivre, inverser en son contraire : l’irréalisme rationnel, selon la prémonition de Nietzsche d’un jour où « le non-vrai sera la condition de la vie », où l’homme ne pourra plus vivre « sans ramener la réalité à la mesure du monde imaginaire de l’inconditionné et de l’identique ».
Ce n’est pas qu’il soit plus difficile de jouer des nombres que des croyances. Mais, en ce jeu-là, le risque est bien plus grand. Car on ne s’implique pas dans les croyances d’autrui lorsqu’on les considère comme un objet d’étude, mais on s’implique nécessairement dans une méthode qui est l’outil même de la connaissance. Le risque est de s’y laisser prendre et, par suite, de s’y perdre. Un long mépris – teinté de pitié – pour ces démarches de l’esprit ne m’a pas toujours retenu d’en être dupe.
Ma seule chance : la règle que je m’étais imposée au départ de ce travail ou, plutôt, l’évidence qui m’était imposée : qu’aucune étude de quelque objet que ce soit ne présente le moindre sens aussi longtemps que le problème de la connaissance n’est pas posé en sa parfaite rigueur.
Sur cette seule base (son premier chapitre) s’est édifiée l’architecture de l’ouvrage, d’une dialectique à l’autre, du plus simple au plus complexe mais sans jamais sortir de l’univers du jeu.
Le fruit de l’effort? Une approche de l’Etre que je ne peux pas dire nouvelle puisque un Platon et Lie tseu, un Ezéchiel et un saint Jean, un Joachim de Flore et un cardinal de Cues, un Spinoza et un Leibnitz en eurent plus que le pressentiment mais que personne encore n’avait formulée en sa méthodique et ludique démarche.

1
LE JEU DES NOMBRES

Aux faux savants que nous sommes le concept d’Unité apparaît le plus simple et le plus évident qui soit, quand il est le plus compliqué, pour ne pas dire le plus incertain.
Voici une table.
Ce disant, j’exclus de cet objet tout ce qui l’augmente ou le réduit sans cesse : de la poussière, des taches de vin, de fruit, un tapis rouge à fleurs, et des brisures, des fêlures, le rabotement du temps, une nette cassure même, visible en ce coin gauche.
A l’inverse, je sous-entends que l’objet est compact, continu, voire homogène, quand je le sais construit de matériels très divers : du bois, de la peinture, le fer des clous, sinon plusieurs bois et plusieurs peintures, des métaux différents, et chaque métal, chaque bois constitué de millions d’atomes autonomes.
Ainsi une table est-elle d’une part le produit, la sommation ou l’ensemble d’une multitude d’existences et, de l’autre, modifiée à tout instant par ce qui s’y ajoute ou s’en retranche. Elle est tout sauf une.
Si je passe d’un objet fabriqué par l’homme, dont l’homme connaît les constituants, à quelque objet organique, tel qu’un arbre, les constituants en seront infiniment plus nombreux, les transformations plus imprévisibles. Mais je ne puis discourir, ni même ouvrir la bouche, ni m’abandonner à la moindre pensée si je n’accepte l’illusion première de l’Unité. Penser : je pense, déjà, n’est-ce pas affirmer que je puis saisir du moins une unité : la mienne?
Or, ce concept de l’1 est si étrange, si controuvé, si peu imaginable ou démontrable en soi qu’il n’est même pas imaginable ou démontrable qu’un homme l’ait conçu en un moment du temps. Quand ai-je pu dire : Je? Fut-ce hier, avant-hier, lorsque j’ai fait l’amour pour la première fois ou quand la barbe m’a poussé? L’adolescent n’est-il pas Je? L’enfant l’est-il? Un singe a-t-il perçu le Un voilà cinq cents millions d’années, un diplodocus, une coquille, une amibe cinq ou six cents millions d’années plus tôt?
L’improbabilité demeure égale, que je traite de l’inventeur de la relativité restreinte ou de son fœtus. Elle croît à mesure que je remonte le temps, ne me laissant plus que cette hypothèse : l’indémontrable concept dut être contemporain de la naissance de la vie, sinon de l’origine de la matière, de l’énergie, de quelque chose que j’ignore, que le savant nomme explosion originelle ou le trou noir et que le croyant nomme Dieu.
Ainsi, à la question paradoxale : d’où me vient l’évidence de l’Unité, n’est-il que deux réponses possibles : cette évidence est illusoire, elle ne correspond à aucune réalité, ou : elle me vient d’ailleurs : d’une antimatière, d’un monde inversé, d’une divinité toute-puissante, infaillible, éternelle, qui serait l’Etre Même, le concept d’Etre en soi.
Ce qui est vrai du concept l’est aussi du principe A = A et, par suite, de tous les concepts, fondés sur le principe d’identité. Si bien que la question première n’est pas autre que celle-ci : cet objet que j’étudie, dans quelle mesure puis-je prétendre à quelque concordance entre la réalité de l’objet et la reconnaissance que je me flatte d’en avoir?
Là encore, dès le départ et dans la suite des âges, à travers tous les philosophes, nous voyons que deux positions extrêmes fournissent à la question les deux réponses contradictoires :
a – le problème n’existe pas. Ce que mes sens ma rapportent de la réalité est la réalité même. Ou : ce que la logique me démontre démontre également la réalité des lois grâce auxquelles j’étudie la réalité. Ou : je sis que mes sens me trompent (par exemple, que les couleurs ne sont pas ce qui est mais, au contraire, le fruit de l’énergie rejetée lors de l’engrènement de la lumière dans la matière) et que ma logique est faillible, incessamment démentie (comme lorsque une même réalité se présente à moi en tant qu’onde et en tant que corpuscule ou lorsque l’électron passe et ne passe pas un seuil déterminé), mais une puissance quelconque, dont je ne veux pas douter (le Progrès irréversible, la dialectique de l’Histoire, le Saint-Esprit) m’assure que, malgré mes erreurs et mon ignorance, je découvrirai un jour la Logique suprême ou le Modèle parfait.
On admettra que, dans ce cas, un mythe préexiste à la connaissance et au reflet sensoriel, à l’effort même d’inventer : le mythe de la Connaissance, du Reflet ou de la Création. Ce mythe, en quelque sorte, a résolu le problème dès l’origine, en l’Etre, si bien que le problème n’a pas lieu d’être posé.
b – le problème est insoluble. Car je ne saurai jamais si la solution que je crois y trouver n’est pas le fruit de ma seule croyance. Mille illusions des sens (le soleil qui tourne autour de la terre, l’éclair qui tombe du ciel) démontrent à celui qui ne croit pas au Reflet la vanité du reflet, mais elles n’éclairent pas l’Observateur. Mille sophismes pris pour des syllogismes, mille tautologies prises pour des certitudes (A = A) montrent à l’Observateur la vanité de la théorie, mais ne convainquent pas l’inventeur de la théorie. L’évidence que toutes les civilisations s’anéantissent un jour, que tous les peuples disparaissent, que tous les projets se dissipent en leur accomplissement révèle à l’Observateur et au Savant la vanité de croire en un quelconque progrès, mais cette évidence ne persuade pas le progressiste, dont le mythe est la Fraternité ou la Justice, l’Amour ou la Liberté.
Entre cet apaisement religieux – naïf – et cette rigueur sceptique, désespérante, que reste-t-il? Le jeu : une quête sans espoir mais sans déception, limitée à des règles dont on sait la gratuité mais apprécie l’exactitude.
Au premier chef le rationaliste (irréaliste) est l’homme du jeu.
Mais les rationalistes eux-mêmes, au cours des âges, n’ont pas joué selon les mêmes règles, ni précisément aux mêmes jeux.

Le bâton-serpent

Nous possédons peu de vestiges du rationalisme akkadien, qui vécut son apogée dans la seconde partie du 3ème millénaire avant J.-C., sinon quelques formules assez reconnaissables :
les dieux n’existent pas, ce ne sont pas eux qui t’ont donné ton rhume, c’est le froid que tu as pris, ce ne sont pas eux qui font que ta femme t’est infidèle, mais ton manque de maîtrise sur elle est le seul coupable;
ou bien : il n’est pas de retour éternel, de la rigole sont nés les vers, du ver toutes les espèces animales, et l’homme, dernier produit de l’évolution, n’est sur terre que pour nourrir le ver de la chair de ses gencives.
Mais nous en savons assez pour définir trois grandes étapes dans ce rationalisme ancien : l’inversion, le cercle et la flèche, les cardinaux.

L’inversion – Lors de la décadence des dernières grandes cités tauriques (Eridu, Warka, Our), une science nouvelle s’impose, celle du Nombre, fondée sur l’inversion.
L’Unité apparaît conçue comme la somme d’un nombre quelconque : a et de son inverse : 1/a.
A + 1/A = (a² + 1)/a = 1.
L’équation est évidemment invérifiable, sauf dans le cas particulier où 1/a = 1-a.
a + 1 – a = 1.
a est ici :
– nécessairement fractionnel de l’Unité,
– définissable comme une inversion : 1/b;
et, par suite, 1/a est définissable comme un nombre entier, b, inverse de l’inversion 1/b.
L’équation peut s’écrire :
b = 1 – 1/b.
Elle conduit à la double identification :
½ = 2;
2 = 1 – ½,
et ½ = -1 :
½ = 1-2 = -1.
2, ½ et -1 sont des valeurs équivalentes.
En généralisant la méthode, on trouve que :
n, 1/n et 1-n sont des valeurs équivalentes.
Tel est le secret de ces étranges calculs où 15 est donné pour le ¼ de l’Unité en même temps que pour le reste : 1 -(1-15).
La triple équation se vérifie pour 1 = 60 :
15 = 60/4
15 = 60-45
15 + (60-15) = 60.
1/4 ou 0,25 égale 15 si 1 = 60
½ ou 0,50 égale 2 si 1 = 4, etc.
Si de tels calculs nous semblent extravagants (ou, à tout le moins abstraits), c’est que nous avons perdu le sens des deux mots-clés du rationalisme akkadien : totalité et partage.
Des écrits approximativement datés de 2400 avant J.-C. restituent ce double sens. Ils ne présentent aucun caractère d’abstraction. L’un traite de la coupe du bois; l’autre d’une redevance fiscale.
Soit une totalité (tronc d’arbre, bambou, bâton) rompue en deux morceaux a et b, comment puis-je mesurer b? Ce ne sera pas en comparant la partie b à la totalité, puisque celle-ci n’existe plus, mais à l’autre partie restante a.
Je dirai par exemple que b est le 1/4 de a, ce qui fait de a une nouvelle unité : 4/4.
L’ancienne totalité : a + b égale alors 4/4 + 1/4 = 5/4, c’est-à-dire que 1 = a + b se formule également : 1 = a + 1/a.
De même, un homme donne les 2/3 de ses biens à son fils aîné et le 1/3 de ses biens au plus jeune. Ou : le prince revendique le 1/3 des biens d’un de ses sujets. Les textes disent qu’alors  le fils aîné ou l’imposé disposent du double restant.
En effet, le 1/3 est le 1/2 de (1-1/3). Si le prince dispose du 1/3, l’imposé garde la disposition des 2/3.
Mais c’est à la condition que 1 (la totalité des biens) égale 2 + 1/2. Toujours :    1 = a + 1/a.
Le calcul est plus évident pour nous si la totalité et l’objet du partage ne sont pas de l’étendue (un bâton) mais de la durée.
L’horloge compte 12 heures. L’heure vécue n’est cependant pas de 1/12 de la durée restante mais son 1/11. 2 heures vécues ne sont plus que les 2/10 ou le 1/5 de la durée restante, etc.
Quand, ainsi, je dis : « il est 1 heure », pour dire qu’une heure est passée, je ne dis pas la réalité : il n’est plus 1 heure ou l’heure 1 est ce qui n’est plus.
Mais je ne dis pas plus vrai lorsque j’affirme : c’est aujourd’hui lundi, alors que ce 1/7 de la semaine, lundi, n’est pas encore vécu dans sa totalité : ce 1/7 n’est pas encore.
Le rapport à la totalité n’est pas dicible, sinon au point 0, que le sumérien et l’akkadien ignorent. De toute façon, il n’est pas non plus de rapport possible entre 0 et un nombre quelconque a (12 ou 7) :
0/a = 0
a/0 = l’infini.
La seule solution est donc bien de comparer b (la partie restante) à son inverse 1/b (la partie vécue). L’unité/totalité 1 (le jour ou la décade) égale b + 1/b.
L’unité vaudra : 11b + 1/11b, ou 10c + 2/10c, ou 9d + 3/9c, c’est-à-dire 12/11 de b ou 6/5 de c ou 4/3 de d à mesure que b = 11/12, c = 5/6, d = ¾ de jour restant à vivre.
Ce calcul pourtant suppose une approximation toujours présente mais occultée ou non en tout calcul où interviennent les concepts de « tout » et de « partie » : une approximation égale à l’inverse du quotum choisi.
La plus grande approximation, au 1/2, correspond de ce fait au partage le plus court : en 2 parties, comme on le vérifie par le partage de la journée en une partie nocturne et une partie diurne.
La nuit couvre 16 heures l’hiver, et le jour 8 heures. Mais, l’été, c’est le jour qui couvre les 16 heures et la nuit les 8 heures. Du solstice d’hiver au solstice d’été, l’approximation joue de 8 heures sur 16, au 1/2.
Dans l’intervalle, du 1/2 à 2, le « jour » se sera fait les 9/15, 10/14, 11/13, 12/12, etc. de la nuit, puis les 13/11, 14/10, 15/9 et 16/8 de la nuit.
C’est-à-dire que, au cours des 24 heures, avec une approximation au 1/24, le bâton n’aura cessé de se rompre en des points de rupture différents : le bâton se sera fait serpent, comme en la main de Moïse, beaucoup plus tard.

Le cercle et la flèche

Historiquement, cette métamorphose a précédé Moïse d’un demi-millénaire. Dès les débuts de la Grande Assyrie, vers 2300 avant J.-C., un symbole apparaît, déjà mythique mais que nous pouvons sans trop de peine rationaliser : la flèche dans le cercle.
Peu après, le Livre des deux chemins témoigne que le nouvel ésotérisme n’est pas ignoré de l’Egypte : de ces deux voies vers le Réel (Roséatou), l’une est la voie directe, de Feu (comme est direct le vol de la flèche), l’autre la voie de l’onde ou du fleuve, la voie d’Eau.
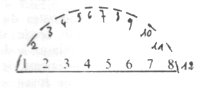
Nous savons que, déjà, existe le cadran solaire ou le demi-cercle, dont le diamètre est comme la corde d’un arc et la demi-circonférence l’arc lui-même. Le faisceau de partage entre la lumière et l’ombre, qui donne l’heure, est la flèche qui les unit.
Déjà, également, s’est posé le problème du rapport existant entre la corde et l’arc. Or, les 12 figurent sur l’arc, le partageant en 11 parties égales, de 1 à 12.
Puis, l’ésotérisme des 8, dominant à l’époque, de l’Ogdoade au panthéon de Memphis, comme en Chine dans le premier Yi King, laisse penser que la voie directe ou « corde » portait ce nombre, qui partageait la corde en 7 parties égales, de 1 à 8.

Il suit que le rapport arc/corde se présentait certainement sous le rapport numérique : (12-1)/(8-1) = 11/7.
Mais le cadran solaire ne révèle l’heure que pendant les 12 heures de « jour ». De l’autre côté du temps, le Soleil ou le Serpent – poursuit sa marche, et le cercle est bouclé. Le rapport de la circonférence totale au diamètre ne peut être alors que 2 X 11/7 = 22/7 ou 3,142.

Les cardinaux – Apogée du rationalisme antique, l’invention des 22/7 = π marque également sa fin. Déjà, le Cercle a renvoyé aux dieux d’Eau ou de Vérité et, plus particulièrement, aux divinités cancériques : l’Hermaï, Seth, le Nash, le Sepher; l’arc et la flèche ont renvoyé aux dieux de Feu ou du Combat et, particulièrement à l’archer sagittaire : Nin, Indra ou Arès, le Rayonnant de Loth, le dieu de l’Arche un jour.
De ce cercle de feu, le foyer, les patriarches et les brahmanes tireront les notions nouvelles de « race », de « tribu », de « famille » ou de « phratrie », où s’éclairera la double énigme de la Totalité et du Partage. Mais ce ne sera plus grâce à la dialectique traditionnelle.
Le dieu de Feu dominera sur le vecteur vertical (accroissement/décroissance) : la flèche. Le dieu d’Eau dominera sur le vecteur horizontal (continuité/discontinuité) : la corde.
Or, nous savons que, deux mille ans plus tôt, les fondateurs des premiers « tells » sumériens (ou des « nomes » en Egypte) partageaient déjà le monde – ou le réel – en ces quatre quartiers, qu’ils nommaient Eléments :

Terre
Eau                                      Air

Feu
Vers 200 avant J.-C. les ésotéristes du Bélier (Amon) renouvellent ce partage à l’intérieur du cercle : ils créent la Rose des Vents, puisque Amon avait été Niaou, le dieu du Souffle.
Pendant cinq siècles, tout l’ésotérisme de Jacob, puis de l’Exode, des Nombres et du Livre de Josué se fondera sur la localisation des 12 (Tribus) aux 4 points cardinaux, selon leurs accroissements (les bénédictions divines) ou réductions (les malédictions) en même temps que sur leurs assimilations (de Lévi et de Siméon) ou désassimilations (Joseph en Ephraïm et Manassé).
Et ce sera encore ce partage/totalité dont Ezéchiel jouera vers 600 avant J.-C. En situant le Feu au Sud et la Terre au Nord, l’Eau à l’occident et l’Air à l’orient, et en localisant 3 des 12 à chaque seuil.
Il faudra que renaisse le rationalisme universel, en Chine et dans l’Inde comme en Grèce et à Rome, au 5ème siècle avant J.-C. pour que les hommes rêvent à nouveau de résoudre l’énigme de l’univers sans se référer à Dieu ou à ses douze Noms.

Les deux cercles
Lorsque Ezéchiel prophétise, à la veille de la captivité de Babylone, puis sous cette captivité, qu’il a prédite, la Tribu n’existe plus, non plus que le merveilleux accord des Justes entre le Tout et la Partie. Mais, de la Justice-foi, il reste ce résidu : la Loi. Cette loi, un Confucius et un Lao tseu en Chine, un Lycurgue, un Solon en Grèce, puis l’Eléate et le Pythagoricien vont se soucier d’abord de la préserver.
Elle ne doit pas être seulement ce condensé de législations : un code que les juges maintenant écrivent, afin d’en conserver la lettre comme l’esprit d’un jugement à l’autre. Mais elle doit être un condensé de « connaissances » universelles grâce auxquelles tous les problèmes trouveront leur solution.
Or, le premier problème qui se pose, en l’éloignement du dieu de Justice, c’est encore – de nouveau – celui du rapport numérique entre le Réel et la raison, qu’on entende par ce mot la « raison juridique » ou seulement logicienne.
Les anciens avaient joué de la flèche et du cercle. Ils en avaient tiré leur constante magique : 11/7 pour le demi-cercle, 22/7 pour le cercle. Et cette découverte n’est pas remise en cause. Mais c’est maintenant le cercle de la Loi qui se présente comme distinct de la réalité, parce que la loi est écrite, immuable et courte, quand les délits et leurs « natures » sont innombrables, quand le coupable et la victime posent à leurs juges des problèmes toujours différents.
Plus généralement, quelle loi, si elle n’est pas d’inspiration divine, peut prétendre à contenir l’infinie diversité et l’infinie mobilité de toutes les formes existantes?
Dans les cinq siècles qui vont suivre, le nouveau rationalisme ne va rien faire d’autre que s’attaquer au dilemme nouveau. Il y emploiera toutes les forces de sa raison et y progressera lentement – par l’invention de ces appareils : la moyenne, le même et l’autre, la quadrature des qualités.
La moyenne – Soit deux cercles a et b (la Loi et le réel). Si je donne au cercle a (la Loi) la valeur même de l’Unité, quelle peut être la valeur de b?
Ou, plus exactement, quel peut être le rapport constant entre le réel et la Loi, entre b et a?
La première solution apparaît vers 500 avant J.-C. et, selon la tradition, Pythagore l’Italique en serait l’inventeur : l’éventualité de l’erreur (on ne dit pas encore : la probabilité) sera réduite au minimum si j’établis la moyenne entre a et b ou 1 et b, en donnant à a la valeur de l’unité même.
La formule est : (1 + B)/2 = C (le troisième cercle/moyenne).
Nous ne savons de façon certaine si Pythagore fut l’inventeur de cette formule, mais il se donnait lui-même pour l’inventeur du Nombre d’or : θ = 1,618.
Il l’avait découvert, sans doute, en inversant la donnée insoluble du problème akkadien : 1 = a + 1/a, en a = 1 +1/a, puisque le nombre θ est le seul nombre qui la vérifie : θ = 1 + 1/θ. 1,618 = 1 + 0,618.
Mais également θ se présente comme la moyenne entre √5 et 1 : (√5 + 1)/2 = θ.
Enfin, le nombre d’or au carré égale le nombre d’or plus l’unité : θ² =θ + 1, et cette égalité n’était pas la moins précieuse pour le mathématicien qui avait découvert que « la diagonale d’un carré, au carré, est égale au double du côté du carré, au carré ».
Puis, en étendant l’équation à tout triangle rectangle, que : « l’hypoténuse au carré est égale à la somme des deux autres côtés au carré ».
En effet, si je donne à ce côté la valeur θ :
θ² = θ + 1.
2 (θ +1) est la valeur de la diagonale au carré, et donc, de l’hypoténuse de tout triangle rectangle dont la somme des autres côtés au carré est 2 (θ + 1).
Puisque θ = (√5 + 1)/2
2 θ = √5 + 1
et 2 (θ +1) = √5 + 1 + 2 = √5 + 3 = 5,236.
On disposait désormais d’un nombre aussi étonnant que les 22/7 de l’Egyptien. Mais, en outre, d’un théorème qui permettait de réduire à une moyenne constante les ondoiements encore angulaires du serpent.
Mais ce n’était qu’une moyenne, utilisable pour calculer l’inscription du carré dans le cercle, en prenant le double du côté du carré comme égal (au carré) au double du rayon (au carré) ou en prenant la diagonale du carré (le diamètre du cercle) comme égal (au carré) au double du côté (au carré).
Or, tous les triangles inscrits dans la moitié du cercle ne sont pas des triangles rectangles. Si leur grand côté ou leur hypoténuse demeure constante (la diagonale du carré et le diamètre du cercle), la somme de leurs côtés au carré ne demeure pas égale à cette hypoténuse au carré; bien que ces côtés s’inscrivent dans des arcs dont la somme égale la moitié du cercle (180 degrés) . (1)

——————————————————————————————-

(1) Si la somme des petits côtés vaut 2 + 4 = 6, la somme de leurs carrés vaut : 4 + 16 = 20. Si la somme des petits carrés vaut 1 + 5 = 6, la somme de leurs carrés vaut : 1 + 25 = 26. Mais le grand côté du triangle rectangle, la diagonale du carré et le diamètre du cercle valent toujours √18, puisque 3² + 3² = 9 + 9 = 18.

Illustration Pierre-Jean Debenat

Le même et l’autre – Ce paradoxe – parmi d’autres, qui en découlaient plus ou moins – passionnait les mathématiciens grecs. Car il était encore une formulation claire de l’insupportable hiatus entre le « système scientifique » et l’innombrable réalité que les Egyptiens avaient cru résoudre en nombrant le rapport constant entre n’importe quelle circonférence d’un cercle (double du cadran solaire) et son diamètre (la corde de l’arc) :
22/7 = 3,142 (ou π à 0,0004 près).
Comme l’Egyptien avait trouvé le rapport entre la droite (corde ou diamètre) et la circonférence du cercle et Pythagore le rapport entre l’inverse et la moyenne, Platon rêvait de découvrir le nombre-clé de l’univers entre le cercle de la Loi (du principe, de l’En-soi) qu’il nommait le cercle du Même, car le Principe est l’Etre même, et le cercle – ou la figure – de la réalité en la diversité des formes, qu’il nommait le cercle de l’Autre, car je ne connais autrui que par une telle figure.
A tort ou à raison, le philosophe imaginait que ce rapport devait être tel qu’il établît un « moyen terme » entre les deux figures/essences du Même et de l’Autre.
Or, les deux univers connus à son époque n’étaient pas encore ceux d’Einstein : la gravitation et l’électromagnétique, ni celui de Dirac et de Pauli : la matière et l’antimatière. Mais seulement l’univers du cercle (lié au rapport 22/7) et celui du triangle rectangle ou du rectangle et du carré (en jouant de la diagonale comme de l’hypoténuse).
Ce que Platon cherchait, en somme, c’était la quadrature du cercle.
Il la trouva.
Si la diagonale au carré égale 2 C² (deux le côté au carré), elle est le double de la surface du carré : S = C².
Quant à la surface du cercle, elle égale le rayon du cercle au carré que multiplie 22/7, puisque 22/7 est le rapport de la circonférence au diamètre.
Si S (la surface du carré) doit égaler S’ (la surface du cercle), il faut que l’équation soit vérifiée : C² = 22 R²/7.
On ne peut qu’imaginer les tâtonnements qui suivirent cette découverte, puisque Platon ne la formulera (dans La République) qu’autour de -370/-368. Né en -430, il aura plus de soixante ans.
Mais, à partir des nombres qu’il donne, il semble assuré que ses deux hypothèses les plus fructueuses aient été les suivantes :
1) le rayon du cercle R = 2. S’ = 22 R²/7 = 88/7 ou 12,57. Le côté du carré vaut alors √12,57.
2) le côté du carré C = 2. C² = S = 4. Le rayon du cercle au carré vaut alors 4 : 22/7 ou (4 X 7)/22 = 28/22 et R = √28/22.
Si cette figure – cercle ou carré – a pour surface le nombre 88/7, la seconde figure vaut: √5 X 12,57 = 28,28 = (9 X22)/7;
C’est un cercle de rayon 3 ou un carré de côté √198/7.
Si la figure a – cercle ou carré – a pour surface le nombre 4, la figure b a pour surface : √5 X ‘ = 8,944 = 9.
C’est un carré de côté 3 ou un cercle de rayon R = √63/22.
Entre ces quatre figures, les nombres de La République témoignent que Platon n’en retint que deux : les deux cercles ou carrés de surface 9 (côté : 3 ou rayon : √63/22) et de surface 88/7 ou 12,57 (rayon : 2 ou côté : √88/7), comme on le constate par l’affirmation célèbre : « Il s’établit entre la génération divine et les générations humaines une correspondance rationnellement exprimable. La base axiomatique (de leurs calculs), accouplée à 5, à la puissance 3, fournit deux harmonies dont l’une est faite d’un nombre constant (le quantum) et de cent multiplié par ce nombre, et dont l’autre est faite :
– partie de 100 carrés de diagonale 5, chacun diminué de 1 (?)
– partie de 100 cubes de 3 ».
La double harmonie « humaine » ne présente aucune difficulté :
100 carrés de diagonale 5 (25 au carré) sont 100 carrés de surface 12,5, à l’approximation près. 100 X 12,5 = 1 250.
100 cubes de 3 égalent : 100 X 9 = 900.
Faute de connaître le quantum du nombre divin, il ne nous est pas permis de déterminer ce nombre aussi directement et l’affirmation de Cicéron doit être considérée avec réserve, que la Grande Année platonicienne vaut 12 954 ans.
Mais nous voyons que le nombre 5 au cube (multiplié par lui-même 3 fois) permet le calcul des deux harmonies. Or, 5³ = 125, et c’est-à-dire que 12,5 n’est pas seulement le carré de diagonale 5 ou la surface 88/7, à l’approximation près, utilisés dans la recherche du nombre humain. C’est aussi le 1/10 de 5 au cube.
Quant à la base axiomatique (l’épitrope grecque) des deux calculs, ce peut être 22/7 ou π approché.
Si bien que, des figures issues du carré de 2 :
4 X √5 = 9
4 X 22/7 = 88/7 ou 12,5
se déduisent, à l’infini, les deux séries :
9 et 12,5 (au 1/10 de l’unité près ou 0,1)
900 et 1 250  (à 10 près)
90 000 et 125 000 (à 1 000 près)
etc.
De sa constante 22/7 l’Egyptien avait tiré une connaissance plus précise des cycles circadiens et annuels, en les fondant sur les 12 heures et les 12 mois. L’ambition de Platon est autre : établir les durées des cycles d’existence des dieux ou des grands mythes de l’humanité, par l’accord de la Forme (l’Autre) et de l’Essence, matière ou principe (le Même). Il ne s’agit donc plus de jours ou d’années mais de siècles et de centaines de siècles.
Il n’en restera pas à cette première approche. Dans le Politique, il invente le concept de précession ou de renversement de sens du Même à l’Autre : toute matière est entropique, elle tend à la mort, par la caducité, hors du pouvoir des dieux et des Idées : c’est la fatalité de la matière durable, contenue dans le principe même de causalité. Mais la forme est résonnante ou récurrente : elle change le révolu en un révolutif et la mort en résurrection.
Dans le Timée, il établit que les deux figures/cercles ne sont pas tangentes, telles que leurs diamètres (et leurs surfaces) puissent s’additionner, mais qu’elles s’inscrivent l’une dans l’autre, comme les deux cercles issus de la bande de Moebius, qu’il donne pour exemple.
En ce lieu même de l’inscription s’instaure l’accord de la Forme et de la Substance en quoi réside la Vie.

Les Qualités – Des inscriptions successives d’un cercle en l’autre le philosophe déduit la série des fractions qui formuleront l’harmonie et dont Jean Diacre dans la chrétienté et Djâbir dans l’Islam tireront au 8ème siècle les structures précises de la science musicale .(2)
Parallèlement, Aristote et ses disciples se fonderont sur les 4 termes platoniciens : l’assimilation, la désassimilation, le plus et le moins, pour formuler leurs Qualités : le sec (qui désassimile), l’humide (qui assimile), le chaud qui augmente les formes ou les volumes, le froid qui les réduit. C’est-à-dire une fois encore, les 4 Eléments : la Terre, l’Eau, le Feu et l’Air, d’où les traités de teinture des métaux, puis l’alchimie déduiront toute leur science.
Et, parallèlement, Hipparque, puis Ptolémée tireront de la notion d’ère précessionnelle 250 + 900 = 2 150 ans) les cycles planétaires qui fonderont l’astronomie, en attendant que l’Apocalypse, puis Mahomet, puis les prophètes du Moyen Age en déduisent la prédiction des deux millénaires à venir.
Mais on voit que, de nouveau, l’apogée du rationalisme hellénistique (au 3ème siècle avant J.-C.) en marque également la corruption. Des 4 Qualités et des 3 Natures se déduisent les 12 de nouveau (4 X 3) : les dieux romains d’abord, mais aussi les 12 apôtres, les 12 Imâms islamiques, les 12 chevaliers de la Table Ronde, les 12 opérations de l’alchimie ou les 7 notes et les 5 silences (les 5 demi-tons plus tard : dièses/bémols).
Tout est à recommencer.

———————————————————————————————-

(2)Les 7 fractions platoniciennes sont, autour de 2²/3 = 4/3 = 1,33 : Fa
3²/2³ = 9/8 = 1,125 : Ré
3⁴/2⁶ = 81/64 = 1,26 pour 5/4 = 1,25 : Mi
et :
3/2 = 1,5 : Sol
3³/2⁴ = 27/16 = 1,69 pour 5/3 = 1,66 : La
3⁵/2⁷ = 243/128 = 1,81 pour 15/8 = 1,8 : Si
Entre les 2 Do, dont le 1er vaut l’Unité et le 2ème  : 2.
L’inversion ou précession se situe dans la progression de 3/2 (Sol) à 3⁴/2⁶ (Mi) autour de Fa.

Les coïncidences
Comme le rationalisme grec a naguère pris son essor en l’épuisement de l’ésotérisme tribal (l’accord partage/totalité), le rationalisme contemporain prend le sien en l’épuisement de l’ésotérisme alchimique : l’accord de la forme/substance, éclatée en « apparence », cette forme sans substance, et en « matière », cette substance sans forme.
Comme le dieu de Justice, jadis, le dieu d’Amour à présent s’éloigne ou se corrompt. Mais le parallélisme entre les deux époques ne se limite pas à cela.
En l’aurore du 17ème siècle, quand renaît l’exigence rationnelle, un mathématicien aussi puissant que Pythagore, Neper, invente le nombre e (2,718) et en fait la base de l’outil nouveau : la mathématique des logarithmes, qui permet de réduire à une progression arithmétique toutes les progressions géométriques concevables.
Au siècle suivant, un autre génie, Euler, donne le nombre (e-1) comme sommation à l’infini de la série des factorielles inverses et invente le concept révolutionnaire de « série convergente » (limitée par un nombre à l’infini). Cent cinquante ans plus tard, le physicien nucléaire donne le même nombre (e-1) comme limite à la vie radioactive de l’isotope .(3)
Il convient de noter que :
a) √(e-1) se déduit de la série platonicienne :
(√12+1)/2 = √5
(√5+1)/2 = θ
(θ +1)/2 = √(e-1).
b) e-1 = 12/7, à la 3ème décimale près : 2,714 pour 2,718.
Si 12/7 égale 1 260 ans, l’Unité : 7/7 égale 900 ans :
900 + 1 260 = 7/7 + 12/7 = 19/7 = e, à l’approximation près.
c) la même science nucléaire fixe aux 6:10 de la vie de l’électron le phénomène de résonance, lié à la « précession de Larmor » qui définit le renversement de sens de la particule à ce moment précis, et cette constatation de même confirme les nombres du Politique et du Timée.
d) l’invention du nombre e se situe exactement une ère précessionnelle après le rationalisme pythagoricien (-530/1620), comme celui-ci s’était situé une ère précessionnelle après l’invention de la constante égyptienne.

——————————————————————————————-

(3) L’isotope est un corps radioactif dont le poids atomique se rapproche de celui d’un corps inscrit dans la table de Mendeleieff comme 228 ou 222 de 226 (le poids atomique du radium). Le mot n’exprime donc, littéralement, que la mise entre parenthèses d’une approximation.

Le Contenant et le Contenu – En son renouveau bimillénaire, le rationalisme renaissant se gausse volontiers de ses prédécesseurs. L’instructeur akkadien de -2400 ne doutait pas de vivre en un temps sans égal, apogée du pouvoir humain; l’aristotélicien de -200 n’en doutait pas davantage, à ce détail près que la Raison tirait son pouvoir du savoir : non plus de la puissance de créer, le Ka, mais de la loi en soi (le Logos).
C’est que le problème qui fut celui du rationalisme précédent se présente au nouveau comme résolu, et que cette solution même, enfantine semble-t-il, ridiculise la recherche acharnée des Anciens.
Depuis Galilée, Neper et Newton, le rationalisme contemporain ne fait pas exception à la règle, bien qu’il tire son savoir de la similitude (les mêmes causes produisent les mêmes effets) ou de quelque autre application des Cercles de Platon d’une part, des Qualités d’Aristote de l’autre.
Mais son problème est inédit, lui semble-t-il. Il ne joue plus de l’arc et de la corde, ou du Même et de l’Autre; il joue du contenant et du contenu. Dans quelle mesure se reflètent-ils et quelle confiance puis-je accorder à ce reflet même sur lequel j’ai fondé ma science?
L’homme du 17ème siècle doute encore – fortement – que des causes puissent être identiques à ce point que je les dise les mêmes, mais l’encyclopédiste feint de n’en point douter (et Kant sera le dernier philosophe qui distinguera le contenant réel du philosophe – la transcendance – du contenant formel qu’il se crée ou qu’il reflète : le transcendantal).
Par la suite, à partir d’Hegel, l’Aristote de notre Kant-Platon, le contenant réel est rejeté au profit du contenant formel (ou la totalité au profit du système). Du nombre d’Avogadro aux principes formulés de la thermodynamique, le savant du siècle dernier ne doute plus de sa victoire, ni de la méthode de base qu’il nomme cartésienne et dont il a gommé le caractère ludique.
Mais l’affinement des 22/7 en π (de 3,142 en 3,1416) ou l’abandon du nombre d’Or (1,618) pour le nombre e-1 (1,718) font que, tout à la fois, je peux ridiculiser les nombres égyptiens et grecs, d’une part, et me prétendre assuré, de l’autre, de mes sinus et de mes cosinus, de mes tangentes et cotangentes, de mes logarithmes (fondées sur le nombre e) et de mes séries de factorielles inverses (fondées sur e-1).
A l’arsenal, un jour – autour de 1900 – s’adjoindra la constante de Planck, h (6,624), puis l’h barré, rayon du cercle de circonférence h : h/2π.
Toute la physique subatomique en sortira, où la matière/masse ne sera plus que l’énergie et où la forme se dissoudra en vibrations, par le calcul de f (la fréquence de l’onde), par son double calcul : f = e/h et f = 1/t.
Ce que cela signifie? Qu’une succession de cercles a, b, c, etc., de rayon ℏ et de circonférence h, peut se présenter comme un jeu de deux ondes orientées inversement.
Les vitesses – égales – de ces deux ondes seront fonction de leur fréquence f et le rapport entre cette fréquence (de l’onde) et l’énergie contenue dans le corpuscule e sera précisément la constante h. C’est-à-dire que : h = e/f ou e = hf.
Comme la vitesse est fonction de la fréquence (v =fl) et la masse fonction de l’énergie : m = e/C², c’est-à-dire, plus généralement, que h, rapport entre l’énergie et la fréquence, est aussi le rapport constant de la masse sur la vitesse : e/f devient : (mC²)/(v/l).
Or, le produit de la masse m par la vitesse v formule la quantité de mouvements du corpuscule, tandis que diverses formules permettent de calculer le « moment cinétique » de l’onde et la charge énergétique du corpuscule à ce moment donné, en se fondant surℏ d’une part, sur la longueur d’onde de l’autre. C’est-à-dire que h est le seul rapport constant entre la quantité de mouvements et la probabilité de position du corpuscule/onde.
Une telle abstraction prête à rire et, dès 1905, dans son Faustroll, Jarry l’avait ridiculisée. Mais il faudra attendre une trentaine d’années pour que le rire éclate : la révélation d’Heisenberg que le nombre h, seul rapport entre la particule et l’onde, entre la masse de l’une et la vitesse de l’autre (ou l’énergie et la fréquence), est également la plus petite erreur possible dans le calcul simultané de l’une et de l’autre.
Le rire était jaune. Il l’est encore chez bon nombre de physiciens. Einstein fut le premier à se réjouir sincèrement, lui pour qui tout « système » n’était que relatif en regard de la totalité; mais, lui-même formulait une totalité qui n’est encore qu’un système : la vitesse de la lumière considérée comme limite absolue de l’Etre et, par suite, non seulement de toutes les vitesses mais de toutes les masses. Si l’énergie atteint un nombre égal à C², m disparaît : e = C². Mais, si m = 0, e n’égale pas C² mais 0. La limite absolue de l’énergie (C²) se présente comme le néant.
Cinquante ans après la formulation du principe d’Heisenberg, son scandale n’est pas vraiment apaisé, ni son rire partagé par tous. Mais la dialectique Planck/Einstein a perdu de sa virulence. Car l’univers de la matière (quantique ou relativisé) n’est plus qu’un contenu en un autre univers : l’antimatière, et, de cette nouvelle dialectique, d’autres ridicules ont surgi.

Matière et antimatière – De même que h, nouveau sésame rationnel (après 22/7, le nombre d’Or, √5 ou e-1), apparaissait comme la plus petite erreur possible dans le double calcul de la position et de la vitesse d’un corpuscule/onde d’énergie e et fréquence f par le rapport e/f = h, on devait en venir à se demander si le sésame einsteinien C² (vitesse de la lumière au carré), rapport entre la masse m et l’énergie e, n’était pas la plus grande erreur possible dans le double calcul de la masse et de l’énergie, jusqu’à l’absurdité parfaite : e = C² quand e = 0 .(4)
C’était imaginer un autre monde, où l’énergie ne posséderait plus une masse, ni la masse, nécessairement, une énergie : la gravitation absolue du trou noir, où toute la lumière se trouverait absorbée.
Un esprit rationnel ne pouvait que refuser de croire en cet autre monde ou, sinon, de croire que cet autre monde pût échapper à l’analyse rationnelle. On imagina donc que « l’autre monde » devait être, à la fois, le même que le nôtre et son inverse : l’antimatière.
Sa « forme » était la même que celle de la matière, mais comme le reflet dans un miroir est identique à son modèle : la gauche à la place de la droite. On nomma ce facteur P (de « parité »).
Sa charge énergétique était la même que celle de la matière (réduite au corpuscule/onde) mais comme une valeur positive peut égaler une valeur négative. On nomma ce facteur C (de « conjugaison » de charge).
Enfin, il évoluait dans un temps semblable au nôtre mais inversé, comme de l’avenir au passé si la matière est censée évoluer du passé à l’avenir. On nomma ce facteur T (« de temps »).
Toute cette belle construction est antérieure à 1963. Car, cette année-là, on s’avisa que les facteurs P et C n’étaient pas utilisables séparément : il n’y avait ni parité ni conjugaison de charge entre ce monde et l’autre. L’hypothèse y succéda (peu de temps) que l’ensemble PC offrait dans les deux mondes une similitude suffisante pour que, pratiquement, il fût utilisable.
Restait le facteur T. Cette symétrie demeura, officiellement, la règle admise jusqu’en 1980, où les Nobels Cronin et Fitch révélèrent au grand public qu’elle était remise en question, à partir d’expériences du reste dont la première remonte à 1963 également.
En clair : ni la gauche ne reproduit exactement la droite (l’étrangeté de l’antimatière n’est pas une réflexion), ni les charges négatives n’inversent rigoureusement les charges positives (l’étrangeté n’est pas une polarité), ni le sens temporel ne s’inverse d’un monde dans l’autre (l’étrangeté n’est pas une simple inversion).
L’antimatière n’est en rien symétrique à la matière, ni en P, ni en C, ni en T. Elle n’est pas une antimatière mais quelque chose de tout différent. Et pourquoi ne serait-ce pas ce que les Anciens nommaient l’Etre, pour le distinguer de l’existence, et Kant encore la Transcendance, pour la distinguer de l’Entendement (transcendantal)? Mahomet nommait cela l’Invisible, pour le distinguer du visible, et l’Islam, tant sunnite que chiite, la table gardée.

——————————————————————————————–

(4) Il faut noter que C, vitesse de la lumière, n’est autre que le rapport entre l’unité électromagnétique (la différence de potentiels absolue) et l’unité électrostatique : 1 C.G.S. (centimètre – gramme – seconde). Approximativement, c = 3. 10¹⁰/1 C.G.S. Pratiquement, on élimine le paradoxe en affirmant que la particule de lumière (photon) est une particule sans masse et qu’un corps doté d’une masse ne peut atteindre à la vitesse de la lumière C.

Jean–Charles PICHON 1982